[This post is part of a series: Piaget, Dewey, and Vertical Learning.]
To learn vertically, we need to be in a state of constant cognitive dissonance. To tolerate a state of constant cognitive dissonance, we need to experience continuous growth and increasing agency. That growth must occur along two parallel tracks: the psychological and the sociological. Without cognitive dissonance, Piaget would say that there is no learning. Without psychological and sociological growth, Dewey would say that there is no education. So, how do we implement vertical learning in today’s society, where most students are “educated” in public schools that impose roles and curriculum on students? If we act strategically, then we rebuild society to create the conditions that enable vertical learning to flourish. Right now, our ability to implement vertical learning is constrained, but as full members of society, it is within our power to change that.
While today’s public schools are not fertile ground for vertical learning, the conditions are not exactly hostile either. A strategic, coherent, independent, active, sense-making teacher can do a lot within present constraints while pushing against those constraints at the same time. Let’s address the curriculum first. In a public school, the curriculum is largely defined by society. This is now happening in the U.S. at the national level, but even when it was happening at the district or classroom level, it was almost always controlled by adults. Some reformers argue that schools can never be effective as long as students don’t control the curriculum, that students won’t learn unless the curriculum is relevant to them. So, what does that mean as we move to adopt Common Core Standards and even more high-stakes testing?
If we are going to implement vertical learning in schools, we need to expand our definitions of curriculum and relevance. Many conflate relevance with choice and intrinsic interest in content. But the middle school students I work with have outgrown the egocentric stage of development and are more concerned with their futures and finding their places in society. In Disrupting Class, Christensen found that students engage in schooling when they can hire schools to be successful. A vertical curriculum in a public school can’t offer much choice, but it can help you grow, prepare for the future, experience sense-making, feel capable, participate as a full member of a vertical learning community, and be your best possible self. Growing into a strategic, coherent, independent, active, sense-making learner is huge. Finding a community where you can be your best possible self is huge. The content of a course is one curriculum, but there is also the psychological curriculum where you learn about yourself and the sociological curriculum where you learn what a society can be and do. In my experience, those last two curricula are highly relevant to all students.
If you are only relying on intrinsic interest in content to make learning relevant, you won’t be very successful. You may engage students initially, but if learning doesn’t go vertical, there will not be psychological growth. The key is going vertical. Unfortunately, it is almost impossible to find curricula today that supports vertical learning. The Common Core Standards in math and the Next Generation Science Standards don’t support it. How can they? Most of us learn horizontally, so those standards have to support horizontal learning. But that ends up reinforcing horizontal learning and discouraging vertical learning. It is still possible to design a vertical curriculum that teaches to those standards, but it is becoming increasingly difficult. When I started teaching math in 1995, I had to meet a set of standards by the end of the year. When I became a science curriculum specialist, our department had to meet a set of standards by the end of a three-year grade span. While constrained, we were still able to design curricula within those constraints that went vertical. But as school districts move toward consistent instruction across classrooms, that flexibility is going away. It is hard to go vertical when you have to teach in lockstep with the horizontal classroom next door.
Another source of concern is the lack of headroom in the curriculum. I think it is possible to design a vertical curriculum that is aligned with standards over three years and that also meets a student’s growth requirements over three years. But, by year five, an independent, active, sense-making learner will have outgrown the standards. A sense-making learner will want to drill deeper and build higher, going well beyond the scope of the standards. An independent learner will want to leverage the learning skills they are developing inside of the classroom to study topics that interest them outside of the classroom. While these students would be capable of learning on their own, they would still benefit from a community that encourages cognitive dissonance, and they would still need support to grow into coherent learners. I functioned as coach and mentor for my students on my own time, but that was only possible because I dedicated the time and chose teaching positions where I never had more than sixty students at once.
As students are growing along the psychological track, they also need to grow along the sociological track. However, the sociological track does not have to be immediately apparent. Instead of presenting my classroom as an exercise in democratic education, I transparently designed systems and structures that made learning the priority. I did not solicit ideas and we did not vote on ideas, but if someone had an idea that would enhance learning, we implemented it. Students learned over time that they could change the design of the learning community as they grew to understand it and became invested in it. When enough students were engaged or major changes were being proposed, we opened things up for general discussion. This approach highlights the importance of Dewey’s parallel tracks.
Imagine that you start working at a company where employees vote on major decisions. Would you feel empowered? I might if the company had a strong culture and if this process had a proven track record. But if this was a new company with all new employees, I’d be worried and annoyed. Even with excellent protocols and facilitators in place, a democratic decision-making process is messy and rarely results in optimal solutions. And before enough people could even begin to learn how to communicate and work together, most people would disengage and stop caring. Now imagine that you start working at a company where the managers listen to and implement good ideas from their employees. At first, employees might be cautious and only submit ideas directly related to their job functions. But if managers truly listened and proved that they were capable of recognizing and implementing good ideas, then employees would get bolder and think bigger. Along the way, they would learn about the business and learn to evaluate ideas from a company-wide perspective. Basically, instead of running the company regardless of capability, you’d play a more active role in running the company as you grew in capability. I believe that this is a better and more authentic way to run a democratic company.
Here is a specific example of how psychological and sociological growth build on one another. In a vertical classroom, everyone is focused on learning and making sense of things because of the systems and structures that have been put in place. Because everyone is learning and making sense of things, everyone is able to contribute to the collective work and progress of the community. Students learn through experience that anyone can and will contribute a critical advance at any time, moving the entire community forward. So, when students work with each other, it is with an extraordinary level of mutual respect; and when students suggest changes to systems and structures in the classroom, it is important to them that those changes continue to enable everyone to participate and contribute fully. This does not come out of a sense of fairness, but from an internalized understanding that the community functions better when everyone has a voice and is encouraged to participate. Losing a voice means that the community is weaker, and decisions and progress will be suboptimal. Without that realization, our desire to find the best answer most efficiently is at odds with our sense of fairness. After that realization, those core values can be aligned and shared. We can’t build a better society until we grow into better individuals.
What happens when the students bump up against constraints not imposed by the teacher, but imposed by the school or society? Well, what happens when I bump against those same constraints myself? As these students grow along the sociological track, they will learn that they have the same power to change schooling and to change society that anyone else does. It’s not a matter of waiting for someone else to clear obstacles for you or to give you an opportunity to make a difference; it’s about growing into and exercising the power you already have. If I created a sandbox without constraints for students to play in sociologically, it wouldn’t be authentic and they’d never learn to be strategic. A sense-making learner understands constraints, a coherent learner understands how to work within constraints, and a strategic learner understands how to work around constraints. If going vertical is something that they care about, then they will work to figure out how to make that happen. It’s what I’m doing.
Friday, June 19, 2015
Saturday, June 13, 2015
Dewey, Society, and Cognitive Development
[This post is part of a series: Piaget, Dewey, and Vertical Learning.]
Dewey makes another critical point that I also brushed aside twenty years ago. He stresses that, for education to be effective, growth must occur along two parallel tracks: the sociological and the psychological. The sociological track is where we learn by participating in society, eventually contributing to society and rebuilding it as an individual. The psychological track is where we come into our own power, growing our capabilities as an individual. When we begin our education, we don’t and can’t know who we want to be or what we want society to be, yet. We need to grow to figure those things out, and we can’t grow psychologically if we don’t grow sociologically, and vice versa.
In Dewey and Society, I wrote that a strategic, coherent, independent, active, sense-making learner will want to rebuild all of the communities and relationships in his life, that he will want to change society. I’m sure that some of you balked at that: “Hey! Not everyone wants to change society. People have different interests, goals, and passions in life.” While that is true, it is also true that you cannot know all of your future interests, goals, and passions based on where you are right now. Are you happy with society as it presently exists? Is there anything you would change about society if you could?
Most of us feel as though we can’t, on our own, change society; we lack the capability. So, we don’t try. And to avoid any cognitive dissonance that might come from that decision, we tell ourselves that we aren’t that interested in changing society. But how can you know whether or not you want to change society if you haven’t even tried to envision what those changes might look like? Our sociological growth is limited by our individual capacity. We won’t consider trying to change society if we don’t think we have the capacity. And, if we can’t change society, we aren’t full members of society, so we hold back from participating and investing in society. But our psychological growth is also limited if we aren’t allowed to change society. If we aren’t allowed to change society, then we limit our aspirations to what society does allow. We dream smaller, and that limits our growth as individuals.
In My Pedagogic Creed, Dewey writes: “I believe that the psychological and social sides are organically related and that education cannot be regarded as a compromise between the two, or a superimposition of one upon the other.” He warns against letting one track take precedence over the other. I ignored that warning twenty years ago, and I ignored it again when I wrote An Introduction to Vertical Learning two months ago.
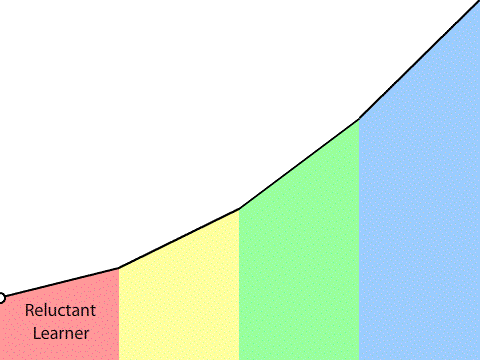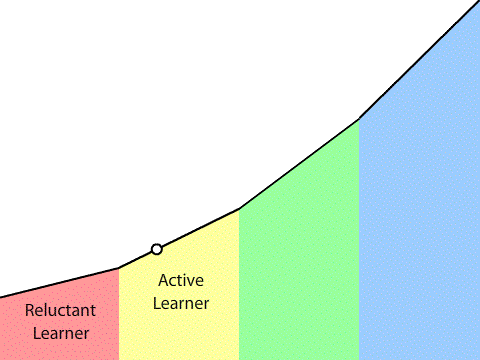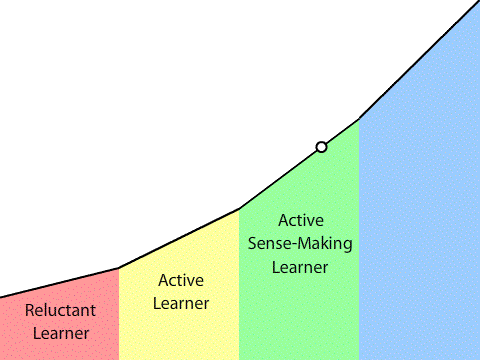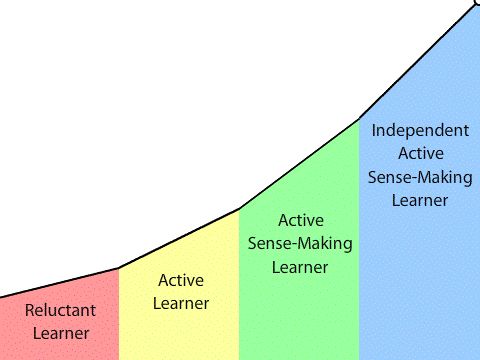
I define vertical learning as a process that takes us through a series of five developmental stages: from reluctant learner to strategic, coherent, independent, active, sense-making learner. I haven’t defined those stages yet (that will have to happen in a separate post), but those stages represent cognitive development, or what Dewey would describe as the psychological track, where we grow into our own power. In defining vertical learning, I didn’t discuss a parallel sociological track. That’s not because one doesn’t exist—my students wouldn’t have gone vertical unless I also nurtured their sociological growth—but because I didn’t recognize that psychological growth cannot occur without sociological growth. (By definition, a strategic thinker is operating in a social context and a full member of society.) I plan on rectifying this in the near future.
Dewey makes another critical point that I also brushed aside twenty years ago. He stresses that, for education to be effective, growth must occur along two parallel tracks: the sociological and the psychological. The sociological track is where we learn by participating in society, eventually contributing to society and rebuilding it as an individual. The psychological track is where we come into our own power, growing our capabilities as an individual. When we begin our education, we don’t and can’t know who we want to be or what we want society to be, yet. We need to grow to figure those things out, and we can’t grow psychologically if we don’t grow sociologically, and vice versa.
In Dewey and Society, I wrote that a strategic, coherent, independent, active, sense-making learner will want to rebuild all of the communities and relationships in his life, that he will want to change society. I’m sure that some of you balked at that: “Hey! Not everyone wants to change society. People have different interests, goals, and passions in life.” While that is true, it is also true that you cannot know all of your future interests, goals, and passions based on where you are right now. Are you happy with society as it presently exists? Is there anything you would change about society if you could?
Most of us feel as though we can’t, on our own, change society; we lack the capability. So, we don’t try. And to avoid any cognitive dissonance that might come from that decision, we tell ourselves that we aren’t that interested in changing society. But how can you know whether or not you want to change society if you haven’t even tried to envision what those changes might look like? Our sociological growth is limited by our individual capacity. We won’t consider trying to change society if we don’t think we have the capacity. And, if we can’t change society, we aren’t full members of society, so we hold back from participating and investing in society. But our psychological growth is also limited if we aren’t allowed to change society. If we aren’t allowed to change society, then we limit our aspirations to what society does allow. We dream smaller, and that limits our growth as individuals.
In My Pedagogic Creed, Dewey writes: “I believe that the psychological and social sides are organically related and that education cannot be regarded as a compromise between the two, or a superimposition of one upon the other.” He warns against letting one track take precedence over the other. I ignored that warning twenty years ago, and I ignored it again when I wrote An Introduction to Vertical Learning two months ago.
I define vertical learning as a process that takes us through a series of five developmental stages: from reluctant learner to strategic, coherent, independent, active, sense-making learner. I haven’t defined those stages yet (that will have to happen in a separate post), but those stages represent cognitive development, or what Dewey would describe as the psychological track, where we grow into our own power. In defining vertical learning, I didn’t discuss a parallel sociological track. That’s not because one doesn’t exist—my students wouldn’t have gone vertical unless I also nurtured their sociological growth—but because I didn’t recognize that psychological growth cannot occur without sociological growth. (By definition, a strategic thinker is operating in a social context and a full member of society.) I plan on rectifying this in the near future.
Thursday, June 11, 2015
Dewey and Society
[This post is part of a series: Piaget, Dewey, and Vertical Learning.]
When I read Dewey twenty years ago and he said that education is a social process, that made sense to me. While we can and do learn on our own, we learn more effectively when we interact with other people. It opens us up to new experiences and viewpoints that can generate cognitive dissonance, which causes us to revise our mental models and learn.
Consider the game Minecraft. Millions of people play Minecraft and learn from each other every day. Now, imagine that the social component of Minecraft did not exist: you could still play Minecraft, but you couldn’t share what you were doing or know what others were doing. People would still play Minecraft, but probably not as many. People would still learn to do new things in Minecraft, but again, probably not as many. Our education in Minecraft is dramatically enhanced when we are an active member of a larger community, even if that community is just one other person.
But Dewey took his thinking much farther than that. He didn’t just say that individuals learn by participating as members of a society; he said that individuals must also participate in creating that society. In My Pedagogic Creed, Dewey writes: “In sum, I believe that the individual who is to be educated is a social individual and that society is an organic union of individuals. If we eliminate the social factor from the child we are left only with an abstraction; if we eliminate the individual factor from society, we are left only with an inert and lifeless mass.” Educating ourselves to participate in a society that we cannot change is a pointless exercise. We aren’t full members of a society we cannot change.
Twenty years ago, I didn’t know what to do with that line of reasoning. I couldn’t translate it into classroom practices, so I assimilated it and brushed it aside. Today, it makes sense to me. For learning to go vertical, you need to be in a state of constant cognitive dissonance. To tolerate a state of constant cognitive dissonance, you need to experience continuous growth and increasing agency. It takes a very special and a very rare community to support and nurture that. If you spend a lot of time with people who constantly make you think and help you grow and do, you notice. And if you are inquisitive, you wonder about it. What makes this community and these relationships different? Why aren’t all of my communities and relationships like this? How can I make all of my communities and relationships better?
Can we learn vertically if we aren’t members of a community that we can change? Of course. You can learn vertically on your own. You can learn vertically using a community as a resource, drawing from it what you need. But if you are participating as a member of a learning community that nurtures vertical learning, eventually you are going to want to change it… and society in general. When you are a reluctant learner, you may ignore the differences between the vertical learning community and the other communities in your life. But those differences will generate cognitive dissonance once you are an independent, active, sense-making learner; and you will want to rebuild your communities once you are a strategic, coherent, independent, active, sense-making learner. If you sense that changing the community is not an option, it places a ceiling on your potential growth and agency, and you won’t tolerate the state of constant cognitive dissonance required to go vertical. In fact, the community will cease being a vertical learning community at all.
When I read Dewey twenty years ago and he said that education is a social process, that made sense to me. While we can and do learn on our own, we learn more effectively when we interact with other people. It opens us up to new experiences and viewpoints that can generate cognitive dissonance, which causes us to revise our mental models and learn.
Consider the game Minecraft. Millions of people play Minecraft and learn from each other every day. Now, imagine that the social component of Minecraft did not exist: you could still play Minecraft, but you couldn’t share what you were doing or know what others were doing. People would still play Minecraft, but probably not as many. People would still learn to do new things in Minecraft, but again, probably not as many. Our education in Minecraft is dramatically enhanced when we are an active member of a larger community, even if that community is just one other person.
But Dewey took his thinking much farther than that. He didn’t just say that individuals learn by participating as members of a society; he said that individuals must also participate in creating that society. In My Pedagogic Creed, Dewey writes: “In sum, I believe that the individual who is to be educated is a social individual and that society is an organic union of individuals. If we eliminate the social factor from the child we are left only with an abstraction; if we eliminate the individual factor from society, we are left only with an inert and lifeless mass.” Educating ourselves to participate in a society that we cannot change is a pointless exercise. We aren’t full members of a society we cannot change.
Twenty years ago, I didn’t know what to do with that line of reasoning. I couldn’t translate it into classroom practices, so I assimilated it and brushed it aside. Today, it makes sense to me. For learning to go vertical, you need to be in a state of constant cognitive dissonance. To tolerate a state of constant cognitive dissonance, you need to experience continuous growth and increasing agency. It takes a very special and a very rare community to support and nurture that. If you spend a lot of time with people who constantly make you think and help you grow and do, you notice. And if you are inquisitive, you wonder about it. What makes this community and these relationships different? Why aren’t all of my communities and relationships like this? How can I make all of my communities and relationships better?
Can we learn vertically if we aren’t members of a community that we can change? Of course. You can learn vertically on your own. You can learn vertically using a community as a resource, drawing from it what you need. But if you are participating as a member of a learning community that nurtures vertical learning, eventually you are going to want to change it… and society in general. When you are a reluctant learner, you may ignore the differences between the vertical learning community and the other communities in your life. But those differences will generate cognitive dissonance once you are an independent, active, sense-making learner; and you will want to rebuild your communities once you are a strategic, coherent, independent, active, sense-making learner. If you sense that changing the community is not an option, it places a ceiling on your potential growth and agency, and you won’t tolerate the state of constant cognitive dissonance required to go vertical. In fact, the community will cease being a vertical learning community at all.
Monday, June 8, 2015
Cognitive Dissonance, Agency, and Growth
[This post is part of a series: Piaget, Dewey, and Vertical Learning.]
Consider cognitive dissonance for a moment. You have a theory that you think is accurate. But now you have to admit to being wrong: your theory is inaccurate. You may have held that theory for years. Other theories may be based on it. It may be central to your world view. It may have taken years for you to develop and you may be immensely proud of it. And now you have to let it go.
When Alec prompted me to reexamine Piaget and Dewey, and I realized that I needed to revise my understanding of their theories, I was happy. I’ve learned to recognize cognitive dissonance as an opportunity for growth and new learning. But that is a learned response. At a much deeper level, cognitive dissonance is still a powerful blow to the ego. Alec and I get together every few months, and I enjoy our conversations because he challenges me to think in new ways. But if he was challenging me daily or weekly, I might grow to resent it. I have resented it. I resent it when I feel like I’m not challenging him in the same way, or when I feel like revising my thinking isn’t enabling us to interact at a higher level. In other words, I resent it when I feel like a little kid learning at someone’s knee and I’m not making much progress.
Alec and I are peers, so that affects how I experience that relationship. Sarah has been my coach for two years. Even though there is no expectation that she will learn from me as I learn from her, it is important to me that she has. But more important is my sense that I’ve been able to internalize the things that I’ve learned, which enables us to take on work that has a much wider scope and impact.
When I first hired Sarah, I had concrete goals in mind. For example, I had the opportunity to pitch one of my ideas to a hundred people in the edtech community. I wasn’t that worried about the pitch itself, but I was scared of the networking that would follow. Sarah suggested that I take some time to think about who I wanted to be at the event and to visualize what that would look like. I then made a plan for myself. While the evening didn’t go exactly according to plan, it went well. At past networking events, I would try to decide what to do in the moment. As the wheels in my head spun, I probably looked like a deer in headlights. By developing a plan ahead of time, I took a lot of thinking (and second guessing) out of the equation and let my reflexes take over. I felt active instead of passive, and this carried over into the energy I brought to each interaction.
If all we had done is work through my concrete goals in a year, I would have considered my time with Sarah very well spent. But as we worked together, I was emboldened to stretch farther and farther, to goals that I had put on the back burner years ago and to goals that I had never even admitted to myself. After working through less than half of my concrete goals, I knew that I had the tools to finish those goals myself and I started setting my sights on bigger targets.
For decades, I have known that I’m at my best when I’m in the moment. I can be very analytical and tend to over think things, hampering my ability to act. When I can turn off that part of my brain for a little while and just be, I’m smarter and happier. There’s always been some tension between the spontaneous person I envision myself to be and the work that I’ve done with Sarah to be more intentional and to use pre-planning to break away from default patterns. I haven’t experienced cognitive dissonance because I’ve viewed this work as transitional: in the future, once I’ve broken old habits and established new ways of being, I’ll be present with myself enough to make all of my decisions in the moment. But recent experiences have made me question that.
It is hard to be in the moment when thinking about everything at the same time. It is hard to work on this blog post if I’m thinking about whether or not blogging is my best, most strategic use of time. And it’s probably not the best time to re-open that discussion when I’m in the midst of struggling with a difficult thought or passage. So how do I know what to think about when?
A week ago, Sarah gave me a little nudge that made me see things differently. What if it’s not about my conscious mind knowing when to plan and when to be in the moment? Maybe it’s about integrating the different parts of myself. At times, I feel like the different parts of myself are battling for dominance. This cacophony makes it hard to function and I rarely feel at peace with my decisions. I’m often happy with an experience after I’ve had it, but almost never happy going into it. This battling takes a huge toll on me. But maybe the parts of myself are battling because they don’t trust that they will get what they need when they need it? If I feed the parts of myself whenever they stand up, maybe they will be happy and learn to manage themselves. This is a new line of thinking for me, but it makes sense. I’m running some experiments to see how well my experiences fit this new mental model.
I wouldn’t have been receptive to Sarah’s nudge if we hadn’t built trust over the years. But I wouldn’t have trusted Sarah if I didn’t sense that she was capable of nudging me in the right places. Being in a state of constant cognitive dissonance is difficult, even when you know that it is good for you. I would say that it is impossible unless you can sense yourself growing and taking on more things. If there was any hint that I was dependent on Sarah and not growing, I would resent and reject her nudges, and our coaching relationship would break down. To be in a state of constant cognitive dissonance, we need to experience agency and growth.
Consider cognitive dissonance for a moment. You have a theory that you think is accurate. But now you have to admit to being wrong: your theory is inaccurate. You may have held that theory for years. Other theories may be based on it. It may be central to your world view. It may have taken years for you to develop and you may be immensely proud of it. And now you have to let it go.
When Alec prompted me to reexamine Piaget and Dewey, and I realized that I needed to revise my understanding of their theories, I was happy. I’ve learned to recognize cognitive dissonance as an opportunity for growth and new learning. But that is a learned response. At a much deeper level, cognitive dissonance is still a powerful blow to the ego. Alec and I get together every few months, and I enjoy our conversations because he challenges me to think in new ways. But if he was challenging me daily or weekly, I might grow to resent it. I have resented it. I resent it when I feel like I’m not challenging him in the same way, or when I feel like revising my thinking isn’t enabling us to interact at a higher level. In other words, I resent it when I feel like a little kid learning at someone’s knee and I’m not making much progress.
Alec and I are peers, so that affects how I experience that relationship. Sarah has been my coach for two years. Even though there is no expectation that she will learn from me as I learn from her, it is important to me that she has. But more important is my sense that I’ve been able to internalize the things that I’ve learned, which enables us to take on work that has a much wider scope and impact.
When I first hired Sarah, I had concrete goals in mind. For example, I had the opportunity to pitch one of my ideas to a hundred people in the edtech community. I wasn’t that worried about the pitch itself, but I was scared of the networking that would follow. Sarah suggested that I take some time to think about who I wanted to be at the event and to visualize what that would look like. I then made a plan for myself. While the evening didn’t go exactly according to plan, it went well. At past networking events, I would try to decide what to do in the moment. As the wheels in my head spun, I probably looked like a deer in headlights. By developing a plan ahead of time, I took a lot of thinking (and second guessing) out of the equation and let my reflexes take over. I felt active instead of passive, and this carried over into the energy I brought to each interaction.
If all we had done is work through my concrete goals in a year, I would have considered my time with Sarah very well spent. But as we worked together, I was emboldened to stretch farther and farther, to goals that I had put on the back burner years ago and to goals that I had never even admitted to myself. After working through less than half of my concrete goals, I knew that I had the tools to finish those goals myself and I started setting my sights on bigger targets.
For decades, I have known that I’m at my best when I’m in the moment. I can be very analytical and tend to over think things, hampering my ability to act. When I can turn off that part of my brain for a little while and just be, I’m smarter and happier. There’s always been some tension between the spontaneous person I envision myself to be and the work that I’ve done with Sarah to be more intentional and to use pre-planning to break away from default patterns. I haven’t experienced cognitive dissonance because I’ve viewed this work as transitional: in the future, once I’ve broken old habits and established new ways of being, I’ll be present with myself enough to make all of my decisions in the moment. But recent experiences have made me question that.
It is hard to be in the moment when thinking about everything at the same time. It is hard to work on this blog post if I’m thinking about whether or not blogging is my best, most strategic use of time. And it’s probably not the best time to re-open that discussion when I’m in the midst of struggling with a difficult thought or passage. So how do I know what to think about when?
A week ago, Sarah gave me a little nudge that made me see things differently. What if it’s not about my conscious mind knowing when to plan and when to be in the moment? Maybe it’s about integrating the different parts of myself. At times, I feel like the different parts of myself are battling for dominance. This cacophony makes it hard to function and I rarely feel at peace with my decisions. I’m often happy with an experience after I’ve had it, but almost never happy going into it. This battling takes a huge toll on me. But maybe the parts of myself are battling because they don’t trust that they will get what they need when they need it? If I feed the parts of myself whenever they stand up, maybe they will be happy and learn to manage themselves. This is a new line of thinking for me, but it makes sense. I’m running some experiments to see how well my experiences fit this new mental model.
I wouldn’t have been receptive to Sarah’s nudge if we hadn’t built trust over the years. But I wouldn’t have trusted Sarah if I didn’t sense that she was capable of nudging me in the right places. Being in a state of constant cognitive dissonance is difficult, even when you know that it is good for you. I would say that it is impossible unless you can sense yourself growing and taking on more things. If there was any hint that I was dependent on Sarah and not growing, I would resent and reject her nudges, and our coaching relationship would break down. To be in a state of constant cognitive dissonance, we need to experience agency and growth.
Friday, June 5, 2015
Piaget and Cognitive Dissonance
[This post is part of a series: Piaget, Dewey, and Vertical Learning.]
One of the core principles of vertical learning is that we learn by constructing and revising mental models. This comes straight out of Piaget’s constructivist learning theory. When I entered the teaching profession in 1995, constructivism was all the rage. Well over half the math teachers I met self-identified as constructivists. But then TERC Investigations and CMP happened, igniting the math wars. The public backlash was enormous, and constructivism was an early casualty.
The failures of TERC Investigations and CMP had nothing to do with constructivism itself. Constructivist learning theory is a theory for how we learn, not a theory for how we should teach. We construct our own understanding whether we are playing with blocks or sitting in a lecture. One learning experience is not inherently superior to the other.
So, what does constructivist learning theory tell us?
Imagine that you have a friend who believes that Democrats always vote to increase the size and power of government. Now, imagine that this mental model is naive: your friend believes that there are no exceptions to his theory even though there are clear cases where his theory does not line up with reality. When your friend is confronted by a discrepancy, he can either deny the discrepancy (assimilation) or note the discrepancy and revise his theory (accommodation). If he is able to revise his mental model so that it fits better and explains more, then his mental model has become more sophisticated.
I believe that the primary role of a teacher is to encourage us to actively test our mental models as widely as possible, and to take note of discrepancies where they exist. If we experience cognitive dissonance, then we will feel compelled to revise and improve our own mental models. But do we need teachers in this equation at all? Can’t we test our models and find discrepancies on our own?
As we grow as learners, we get better at testing our models and detecting discrepancies. Where reluctant learners avoid cognitive dissonance, independent active learners seek out and embrace cognitive dissonance. But I don’t think we ever reach a point where we can see everything ourselves. We may not need a formal teacher, but we do need to interact with people who can point out our blind spots. For example, I thought I knew Piaget and Dewey well. It wasn’t until my friend Alec gave me a nudge that I questioned that belief and uncovered that I didn’t know Piaget and Dewey nearly as well as I thought. I don’t think I was being defensive and avoiding discrepancies; I just thought I was too busy to go back and double check every little thing. Now I’m glad that I did.
One of the core principles of vertical learning is that we learn by constructing and revising mental models. This comes straight out of Piaget’s constructivist learning theory. When I entered the teaching profession in 1995, constructivism was all the rage. Well over half the math teachers I met self-identified as constructivists. But then TERC Investigations and CMP happened, igniting the math wars. The public backlash was enormous, and constructivism was an early casualty.
The failures of TERC Investigations and CMP had nothing to do with constructivism itself. Constructivist learning theory is a theory for how we learn, not a theory for how we should teach. We construct our own understanding whether we are playing with blocks or sitting in a lecture. One learning experience is not inherently superior to the other.
So, what does constructivist learning theory tell us?
- We construct our own understanding by developing internal theories (mental models or schema) to explain our experiences.
- Two people having the same experience may not use or develop the same mental models to explain it. We explain our experiences differently.
- We force new experiences to fit into existing mental models using a process called assimilation.
- We experience cognitive dissonance when we notice discrepancies between our experiences and our mental models.
- If we experience cognitive dissonance, we attempt to revise our mental models to better fit our experiences using a process called accommodation.
Imagine that you have a friend who believes that Democrats always vote to increase the size and power of government. Now, imagine that this mental model is naive: your friend believes that there are no exceptions to his theory even though there are clear cases where his theory does not line up with reality. When your friend is confronted by a discrepancy, he can either deny the discrepancy (assimilation) or note the discrepancy and revise his theory (accommodation). If he is able to revise his mental model so that it fits better and explains more, then his mental model has become more sophisticated.
I believe that the primary role of a teacher is to encourage us to actively test our mental models as widely as possible, and to take note of discrepancies where they exist. If we experience cognitive dissonance, then we will feel compelled to revise and improve our own mental models. But do we need teachers in this equation at all? Can’t we test our models and find discrepancies on our own?
As we grow as learners, we get better at testing our models and detecting discrepancies. Where reluctant learners avoid cognitive dissonance, independent active learners seek out and embrace cognitive dissonance. But I don’t think we ever reach a point where we can see everything ourselves. We may not need a formal teacher, but we do need to interact with people who can point out our blind spots. For example, I thought I knew Piaget and Dewey well. It wasn’t until my friend Alec gave me a nudge that I questioned that belief and uncovered that I didn’t know Piaget and Dewey nearly as well as I thought. I don’t think I was being defensive and avoiding discrepancies; I just thought I was too busy to go back and double check every little thing. Now I’m glad that I did.
Thursday, June 4, 2015
Piaget, Dewey, and Vertical Learning
I had dinner with my friend Alec a few weeks ago. After reading An Introduction to Vertical Learning, he asked me how I saw vertical learning sitting relative to Piaget and Dewey. Jean Piaget was a Swiss psychologist and philosopher who believed that we generate meaning through the interaction of our experiences and ideas, and that cognitive development occurs through a series of stages. John Dewey was an American psychologist and philosopher who had a profound belief in democracy. He believed that education and learning are social and interactive processes, and that all students should take an active role in their own learning.
Vertical learning is firmly grounded in Piaget’s constructivist learning theory. It is designed to encourage students to become independent active learners by seeking out and embracing cognitive dissonance. Dewey’s influence on vertical learning is less direct. Like Dewey, I believe that the purpose of education is not to acquire a pre-determined set of skills, but to realize one’s full potential. On the surface it may have appeared as though my students were studying math and science, but they knew that they were actually building their capacity to learn in general. Without that sense of relevance, they would have never taken ownership of their own learning and gone vertical. You could say that I was using Piaget’s engine to drive us to Dewey’s destination.
Alec’s question prompted me to brush up on Piaget and Dewey. Ideas that I thought I knew well took on new meanings once I examined them again through twenty years of experience and a more sophisticated set of mental models. This cognitive dissonance is causing me to revise my own thinking once more. This is still a work in progress, but here are some of my recent thoughts on Piaget and Dewey.
Piaget and Cognitive Dissonance
Cognitive Dissonance, Agency, and Growth
Dewey and Society
Dewey, Society, and Cognitive Development
Vertical Learning and Constraints
Vertical learning is firmly grounded in Piaget’s constructivist learning theory. It is designed to encourage students to become independent active learners by seeking out and embracing cognitive dissonance. Dewey’s influence on vertical learning is less direct. Like Dewey, I believe that the purpose of education is not to acquire a pre-determined set of skills, but to realize one’s full potential. On the surface it may have appeared as though my students were studying math and science, but they knew that they were actually building their capacity to learn in general. Without that sense of relevance, they would have never taken ownership of their own learning and gone vertical. You could say that I was using Piaget’s engine to drive us to Dewey’s destination.
Alec’s question prompted me to brush up on Piaget and Dewey. Ideas that I thought I knew well took on new meanings once I examined them again through twenty years of experience and a more sophisticated set of mental models. This cognitive dissonance is causing me to revise my own thinking once more. This is still a work in progress, but here are some of my recent thoughts on Piaget and Dewey.
Piaget and Cognitive Dissonance
Cognitive Dissonance, Agency, and Growth
Dewey and Society
Dewey, Society, and Cognitive Development
Vertical Learning and Constraints
Tuesday, June 2, 2015
On My Birthday
I celebrated my 46th birthday two weeks ago. I haven’t celebrated my birthday on my birthday in over ten years. I usually have dinner with my family on the weekend. We’ll have a cake, and my niece and nephew will make me cards, but my birthday is folded in with Mother’s Day and I am resolutely not the center of attention. I usually spend a day with my friend Kerry some time in May. Our birthdays are both in May, and we use the occasion to slow down, hang out, and catch up. But nothing on the day itself.
In the weeks leading up to my birthday, well-wishers inevitably ask me what I’m doing that day. I’ll deflect and say that I’m too old to celebrate my birthday, that getting one year older isn’t something that I want to celebrate. They’ll tell me that I’m being silly and that I should do something fun. I’ll smile and shake my head ruefully. But this year was a little different. Relatives flew into town for a graduation, and I don’t know if it’s because they grew up in Mississippi, but they were shockingly warm and caring. The number of people insisting that I do something special on my birthday doubled, and it must have had an impact on me because, when I went to bed the night before my birthday, I suddenly wanted to mark the occasion. How? I had no idea.
In the morning, I woke up to find a lengthy email from my sister Carol, and a half dozen birthday wishes posted on my Facebook wall. Over the course of the day, a few more emails and another half dozen Facebook posts came in. I also got a phone call from my parents. I had the second of two birthday cupcakes from my sister Lisa for breakfast. Then at around noon, I sat down to work at my computer. I had recently taken on two freelance projects, and both projects were coming down to the wire. Deadlines were tight and team members were depending on me. I worked until 7:50 PM, taking a few lengthy breaks for lunch, to go on a walk, and to clean my kitchen. After work, I had dinner, responded to everyone who had sent me birthday wishes, took a midnight stroll, and then wrote in my gratitude journal.
As I sat down to write in my gratitude journal, I felt a warm, radiating sensation in my body. I was glowing with happiness. When I tried to identify the source of my happiness, the first thought that popped into my head was that I felt “well-taken care of.” What did that even mean? As I probed deeper, a second thought popped into my head. This second thought was so far outside my normal way of being that I was reluctant to commit it to paper. But I did. I wrote that I felt “loved and well-connected.”
Let me tackle the second thought first. A few months ago, I reconnected with an old friend through Facebook. Zmira is Israeli. We worked together at the Jewish Community Day School and, even though she was the visitor in a foreign land, she sort of adopted me. The whole community at JCDS sort of adopted me. I was constantly being invited over to Shabbat dinner by people whom I barely even knew as work friends. But when Zmira returned to Israel and I left JCDS, we fell out of touch and I disconnected from the JCDS community. Reconnecting with Zmira through Facebook restored this old network. And this old network didn’t know or care that I had stopped celebrating my birthday. Old friends just posted birthday wishes on my wall. But here’s the weird thing. Current friends who had stopped trying to send me birthday wishes over the years were suddenly posting on my wall, too. It was this sudden and completely unexpected outpouring that made me feel incredibly loved and well-connected.
Now back to the first thought. It is hard to reconcile feeling “well-taken care of” while working on my birthday, going through my regular routine, and not speaking to a soul all day other than my parents. When I woke up that morning, I was concerned that my little voice was going to throw a tantrum because I decided to mark my birthday the night before, but I had already committed to a full day of work in my weekly plan. My little voice was going to be upset no matter what I chose to do. So, I woke up that morning determined to be extra kind and attentive to my little voice. I let him know that his needs took priority. I planned to work, but we would spend time together doing a few special things, and I was prepared to ditch work at a moment’s notice.
I am normally a bit dismissive and disdainful of my little voice. He shows up to nag me at the worst possible times. So, my concern and attentiveness must have been disarming because he agreed that working made sense as long as I took frequent breaks and promised to stop working by 8:00 PM. Together, we outlined some of the special things that we would do together. The top priority was responding to each birthday wish with warmth and gratitude. We really looked forward to it. We also planned an extra long midnight stroll and a special birthday dinner. My parents had given me spareribs and two beautiful fresh green peppers. I love green peppers, but hadn’t prepared them with black bean and garlic sauce in ages. It was the perfect comfort food for my birthday. With the day mapped out, my little voice was content, but I was still concerned. So I checked in on him constantly, maintaining a running dialogue with him as I worked. This made my little voice very happy. And I was happy, too. We both felt “well-taken care of.”
There are a few things that I took away from my birthday celebration. The first is that I’m rarely present with myself. I’m happiest and at my best when I’m present with other people, especially kids. But when I’m by myself, I associate being in the moment as getting lost in the moment and entering a flow state. When I started my midnight strolls, going for a walk at 3:00 AM on a warm summer night in a t-shirt, shorts, and sandals, I wrote about the serenity I feel as my senses open wide to take everything in. But I am there, too. Noting my own pleasure makes me smile and laugh inside. I need to be present with myself more often.
The second thing that I took away was the need to acknowledge the positive things that I have in my life. The love and connections represented by those birthday wishes didn’t just materialize out of thin air. They existed the day before my birthday, too. But I hadn’t acknowledge them until they manifested themselves in an unmistakable way on my birthday. What if I acknowledged and experienced that love and those connections on a daily basis?
My third takeaway is something that I’ve been working at for a long time, but I still have a long way to go. One of my daily practices is writing in my gratitude journal. For 15 minutes a day, I am present with myself as I acknowledge the things that make me grateful. I am grateful for many things, but I tend not to acknowledge the role that I play in any of it. I noticed that I was doing this again as I was writing the fifth paragraph of this blog post. I had a hand in creating those connections, too. Zmira and I adopted each other, and the JCDS community and I embraced each other. It wasn’t by accident that they decided to make the secular math teacher the 7th- and 8th-grade homeroom teacher for the school. I can be a bit odd, but I’m a good friend. Sometimes I need to acknowledge how awesome I am.
Happy birthday, kid! Be good to yourself and stop deflecting! :)
In the weeks leading up to my birthday, well-wishers inevitably ask me what I’m doing that day. I’ll deflect and say that I’m too old to celebrate my birthday, that getting one year older isn’t something that I want to celebrate. They’ll tell me that I’m being silly and that I should do something fun. I’ll smile and shake my head ruefully. But this year was a little different. Relatives flew into town for a graduation, and I don’t know if it’s because they grew up in Mississippi, but they were shockingly warm and caring. The number of people insisting that I do something special on my birthday doubled, and it must have had an impact on me because, when I went to bed the night before my birthday, I suddenly wanted to mark the occasion. How? I had no idea.
In the morning, I woke up to find a lengthy email from my sister Carol, and a half dozen birthday wishes posted on my Facebook wall. Over the course of the day, a few more emails and another half dozen Facebook posts came in. I also got a phone call from my parents. I had the second of two birthday cupcakes from my sister Lisa for breakfast. Then at around noon, I sat down to work at my computer. I had recently taken on two freelance projects, and both projects were coming down to the wire. Deadlines were tight and team members were depending on me. I worked until 7:50 PM, taking a few lengthy breaks for lunch, to go on a walk, and to clean my kitchen. After work, I had dinner, responded to everyone who had sent me birthday wishes, took a midnight stroll, and then wrote in my gratitude journal.
As I sat down to write in my gratitude journal, I felt a warm, radiating sensation in my body. I was glowing with happiness. When I tried to identify the source of my happiness, the first thought that popped into my head was that I felt “well-taken care of.” What did that even mean? As I probed deeper, a second thought popped into my head. This second thought was so far outside my normal way of being that I was reluctant to commit it to paper. But I did. I wrote that I felt “loved and well-connected.”
Let me tackle the second thought first. A few months ago, I reconnected with an old friend through Facebook. Zmira is Israeli. We worked together at the Jewish Community Day School and, even though she was the visitor in a foreign land, she sort of adopted me. The whole community at JCDS sort of adopted me. I was constantly being invited over to Shabbat dinner by people whom I barely even knew as work friends. But when Zmira returned to Israel and I left JCDS, we fell out of touch and I disconnected from the JCDS community. Reconnecting with Zmira through Facebook restored this old network. And this old network didn’t know or care that I had stopped celebrating my birthday. Old friends just posted birthday wishes on my wall. But here’s the weird thing. Current friends who had stopped trying to send me birthday wishes over the years were suddenly posting on my wall, too. It was this sudden and completely unexpected outpouring that made me feel incredibly loved and well-connected.
Now back to the first thought. It is hard to reconcile feeling “well-taken care of” while working on my birthday, going through my regular routine, and not speaking to a soul all day other than my parents. When I woke up that morning, I was concerned that my little voice was going to throw a tantrum because I decided to mark my birthday the night before, but I had already committed to a full day of work in my weekly plan. My little voice was going to be upset no matter what I chose to do. So, I woke up that morning determined to be extra kind and attentive to my little voice. I let him know that his needs took priority. I planned to work, but we would spend time together doing a few special things, and I was prepared to ditch work at a moment’s notice.
I am normally a bit dismissive and disdainful of my little voice. He shows up to nag me at the worst possible times. So, my concern and attentiveness must have been disarming because he agreed that working made sense as long as I took frequent breaks and promised to stop working by 8:00 PM. Together, we outlined some of the special things that we would do together. The top priority was responding to each birthday wish with warmth and gratitude. We really looked forward to it. We also planned an extra long midnight stroll and a special birthday dinner. My parents had given me spareribs and two beautiful fresh green peppers. I love green peppers, but hadn’t prepared them with black bean and garlic sauce in ages. It was the perfect comfort food for my birthday. With the day mapped out, my little voice was content, but I was still concerned. So I checked in on him constantly, maintaining a running dialogue with him as I worked. This made my little voice very happy. And I was happy, too. We both felt “well-taken care of.”
There are a few things that I took away from my birthday celebration. The first is that I’m rarely present with myself. I’m happiest and at my best when I’m present with other people, especially kids. But when I’m by myself, I associate being in the moment as getting lost in the moment and entering a flow state. When I started my midnight strolls, going for a walk at 3:00 AM on a warm summer night in a t-shirt, shorts, and sandals, I wrote about the serenity I feel as my senses open wide to take everything in. But I am there, too. Noting my own pleasure makes me smile and laugh inside. I need to be present with myself more often.
The second thing that I took away was the need to acknowledge the positive things that I have in my life. The love and connections represented by those birthday wishes didn’t just materialize out of thin air. They existed the day before my birthday, too. But I hadn’t acknowledge them until they manifested themselves in an unmistakable way on my birthday. What if I acknowledged and experienced that love and those connections on a daily basis?
My third takeaway is something that I’ve been working at for a long time, but I still have a long way to go. One of my daily practices is writing in my gratitude journal. For 15 minutes a day, I am present with myself as I acknowledge the things that make me grateful. I am grateful for many things, but I tend not to acknowledge the role that I play in any of it. I noticed that I was doing this again as I was writing the fifth paragraph of this blog post. I had a hand in creating those connections, too. Zmira and I adopted each other, and the JCDS community and I embraced each other. It wasn’t by accident that they decided to make the secular math teacher the 7th- and 8th-grade homeroom teacher for the school. I can be a bit odd, but I’m a good friend. Sometimes I need to acknowledge how awesome I am.
Happy birthday, kid! Be good to yourself and stop deflecting! :)
Monday, April 13, 2015
An Introduction to Vertical Learning
What Is Vertical Learning?
We learn vertically when we revise mental models by building up and drilling down. Vertical learning is a theory and set of design principles for creating learning experiences that enable and encourage us to grow as independent vertical learners in all facets of our lives.
Revising Mental Models
We learn by constructing and revising mental models. A mental model is an internal theory for how and why something works. New mental models are naive. Mental models only become sophisticated and powerful once they have been applied and revised over time. We revise mental models when they don’t work reliably, we encounter edge cases, we apply them in new contexts, or we recognize that several separate models can be unified into one general model.
Building Up, Drilling Down
A vertical curriculum enables us to learn vertically by maximizing the opportunities we have to revise our mental models. Instead of constructing new mental models to learn something new, we leverage and build on existing mental models. By constantly leveraging and building on a core set of models, we apply and revise those models repeatedly in new contexts over time, increasing the sophistication of our understanding and developing skills that we can use to revise other mental models. We build up when we leverage a mental model to learn something new, and we drill down when we revise a mental model to understand something better.
Apples and Bananas
Most of us have sophisticated and robust mental models for thinking about collections of objects. We work with collections every day and we have a wealth of experience with them. These mental models are so sophisticated that we can use them to think about apples and bananas in baskets even if we have never worked with apples and bananas in baskets before. By leveraging and building on an existing sophisticated mental model, and revising that mental model by applying it in a series of increasingly complex scenarios, students are able to construct a sophisticated understanding of the distributive property in one lesson.
Want them to start from the inside and work their way out? Want them to start from the outside and work their way in? How about starting somewhere in the middle? No problem. Their mental model is flexible and sophisticated enough to handle it.
I have taught this lesson to hundreds of students and, within 30 minutes and without exception, every one of them has been able to simplify expressions like the one below, and explain and justify their reasoning while doing it. Students are remarkably capable when applying sophisticated mental models. They are unsurprisingly less capable when applying mental models that are new and naive.
Scalability and Leverage
A vertical curriculum is designed around mental models that scale and have leverage. Mental models that scale have room to grow and can be revised and applied over many years. Mental models that have leverage can be applied in many contexts and used to learn new things.
Noted physicist and educator Richard Feynman once wrote: “If, in some cataclysm, all scientific knowledge were to be destroyed, and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis (or the atomic fact, or whatever you wish to call it) that all things are made of atoms—little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied.”
In Chemistry from the Ground Up, we drill down into the atomic hypothesis by investigating how and why molecules attract each other, and build up by leveraging our revised mental model to construct sophisticated understandings of states of matter, evaporation and condensation, phase transitions, chemical reactions, solubility, and cell chemistry on top of it.
 |
| Mental models go from yellow to green to blue as they increase in sophistication |
In a series of lessons I call Applying Statistical Mechanics to Model Dynamic Systems with Net Flows down Gradients, we apply the atomic hypothesis by drilling down into diffusion and modeling particles moving around in perpetual motion with pennies. Instead of leveraging an existing mental model that is already sophisticated, as in Apples and Bananas, this time we are taking a naive mental model and revising it over time so that it becomes sophisticated.
As we drill down and unpack diffusion, our understanding deepens and our mental model gains new dimensions and detail. The process of drilling down makes a model less opaque as we begin to detect and understand the underlying mechanisms. From there, we then use the mental model we have constructed to understand diffusion as a shared foundation to build up and construct a more sophisticated understanding of electrical circuits, fluid flow, and heat transfer. Along the way, we revise our mental models dozens of times and, because these mental models are constructed on top of one another, each time we revise one of them, we revise them all.
Journeying to a New Mountain
Revising a mental model can be scary and difficult. The analogy I use is journeying from one mountain to another.
Imagine that you are on a mountain. This is your existing mental model. Life is pretty good on top of this mountain, and it took a lot of hard work to get to where you are now. In the distance, you think you see a taller and better mountain, but you can’t be sure. Between you and this new mountain is a treacherous valley. Not only is the terrain in the valley incredibly difficult to traverse, the valley is also enshrouded in fog. Once you descend into the valley, you lose all sense of direction and can easily get turned around.
Providing students with opportunities to revise their mental models is not enough. We also have to encourage them to descend into the valley. Reluctant learners are reluctant to descend into the valley because the journey looks risky (it’s difficult and dangerous, and we might not make it) and the rewards uncertain (is the new mountain really taller and better than the current mountain?).
To make a journey safer, pick a mountain that is close and a path where the terrain is easy. In Applying Statistical Mechanics, we start by modeling diffusion by flipping pennies. This model is concrete and transparent. The mechanics of the model are intuitive and make sense, and students have a “360-degree” view of everything that happens. They can watch what is happening on the macroscopic scale, drill down to the molecular scale, and connect the two. The experience is also immersive. Students are surrounded by visual data with clear and immediate feedback. All of this makes analyzing and understanding diffusion easier and more accessible.
To make a journey more rewarding, pick a mountain that is tall and has a good view of a bunch of even taller mountains. We feel pleased and satisfied when we scale a tall mountain and our mental model makes more sense, and we feel powerful when our mental model has more leverage and exciting new destinations are suddenly within our reach. Leverage can’t be theoretical; it has to be experienced. Students experience that leverage by drilling down into diffusion and then leveraging their mental model to understand electrical circuits, fluid flow, and heat transfer. But they also experience that leverage by conducting their own investigations and solving their own application problems.
Think of the destinations that we can see and reach easily from our current position as a sandbox we can explore and play in. That sandbox should expand each time we scale a new mountain because our new mountain is taller (we can see farther) and we are getting more skilled at traversing the valley (we can travel farther, faster, and over more difficult terrain). Otherwise, what’s the point? If a journey is safe but unrewarding, we may go on the first journey, but we won’t go on a second.
By guiding reluctant learners on safe journeys to mountains with leverage, we supply them with experiences and new data that can shift their risk-reward calculations and help them become active learners. Active learners actively test and evaluate their mental models, seeking out edge cases and new contexts where their mental models might fail, so that they can revise their mental models and improve their understanding. Active learners don’t avoid the valley, they descend into the valley eager to reach the next mountain.
Shifting Gears
How do we know if we are learning vertically? Vertical learners pass through a number of shifts. I call them gear shifts. A gear shift is a major expansion in our ability to perceive and pursue opportunities.
The first gear shift is the shift from reluctant to active learner. My most reluctant learners typically shift into active learners in six months. “I’m not sure I understand how to do that problem. Can I come up to the board and figure it out?” “I think I understand it but I’m not sure. Can you give me a really hard problem so that I can test myself?” I hear those two requests over and over again. As active learners, my students would take the initiative to make sure they understood what we were doing, but they still relied on me to guide them. They couldn’t navigate their way through the valley to the next mountain on their own, but they were eager to follow someone who could.
After three years, some of my students shifted gears again. They shifted from active learners to sense-making learners. They knew when something made sense and when it didn’t, and they knew which way to head in the valley even though it was enshrouded in fog. But they weren’t confident in their ability to traverse the terrain. So while they would try to steer the class in the right direction, they wouldn’t strike off on their own if the class was heading the wrong way.
The next gear shift is from sense-making learner to independent learner. In this gear, we are determined to make sense of things, typically in a specific domain. We have built up and drilled down so far, and our thinking in that domain is so sophisticated, that it nags at us when something doesn’t make sense or one of our mental models isn’t integrated and grounded with the rest. None of my students shifted to independent learner while I was their teacher, but I believe that they would have in time. Consider how far they did shift in three years or less, and from inside a school system that doesn’t nurture vertical learning. Imagine what students could do in ten years in a school system and society that does nurture vertical learning.
As we learn vertically, we grow and shift gears; and as we shift gears, we learn vertically in more facets of our lives.
Vertical Learning as Theory
- We learn by constructing and revising mental models.
- Mental models only become sophisticated and powerful once they have been applied and revised over time.
- We build up when we leverage a mental model to learn something new, and we drill down when we revise a mental model to understand something better.
- Leveraging and building up from an existing sophisticated mental model enables us to construct new understandings that are also sophisticated.
- Drilling down into a mental model makes the model less opaque as we unpack it and begin to detect and understand the underlying mechanisms.
- When we construct mental models on top of one another and revise one of them, we revise them all.
- We are motivated to revise mental models when our risk-reward analysis is favorable. Our risk-reward analysis is based on data from past experiences.
- Revising mental models is easier when underlying mechanisms are concrete and transparent, and data and feedback are clear and immediate.
- We feel pleased and satisfied when our mental models make more sense, and we feel powerful when our mental models have more leverage.
- Our ability to perceive and pursue opportunities increases as the sophistication of our mental models and our ability to revise them increase.
Vertical Learning as Design Principles
- Construct mental models that scale and have leverage.
- Enable and encourage students to revise mental models.
- Apply mental models in increasingly sophisticated contexts.
- Leverage and build on a core set of mental models over time to learn new things.
- Create learning experiences that are concrete, transparent, and immersive.
- Sequence learning experiences so that, by revising their mental models, students build sophistication and leverage for the next experience.
- Encourage inquiry and enable students to conduct their own investigations and solve their own application problems.
- Provide opportunities for students to reflect on and internalize their experiences.
- Develop learning communities where students are peers and learning is explicit and the priority.
- Use the occurrence of gear shifts to evaluate your design.
Vertical Learning as Mental Model
Vertical learning builds on a number of existing learning theories. I didn’t develop vertical learning because those theories are wrong. I developed vertical learning because those theories are too naive to help me figure out how to enable and encourage students to revise their mental models and shift gears. For the past twenty years, I applied and revised existing learning theories, building up and drilling down in an attempt to construct a more sophisticated understanding of how we learn and grow. Vertical learning is the result.
Vertical learning is very much a work-in-progress. It’s still not nearly sophisticated enough. But it has reached the point where I’m ready to talk about it. But how do you talk about a theory that’s been revised for twenty years behind closed doors? Once again, I find myself following Richard Feynman’s lead. This post is a little wordier than Feynman’s atomic hypothesis, but it serves the same purpose. Think of this post as a launching point. In this one post, you will see, there is an enormous amount of information about how we learn and grow, if just a little imagination and thinking are applied.
Drill down and build up. I’ll see you on the next mountain!
Wednesday, February 11, 2015
Statistical Mechanics, Summary
[This blog post is part of two series. The first series, titled Statistical Mechanics, is a series of lessons that I have developed to illustrate how curriculum and instruction can be designed to encourage vertical learning. We start by drilling down from our understanding of diffusion to develop a dynamic model of diffusion grounded in random particle motion using statistical mechanics. We then build on top of this foundation to construct deeper understandings of fluid flow, heat transfer, and electrical circuits. You can navigate through the lessons in this series using the links below. These lessons are then part of a larger series, Defining Vertical Learning.]
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
A mental model is our internal theory for how and why something works. We learn when we construct new mental models and revise old ones. Even when we read something in a textbook or hear something in a lecture, we don’t actually learn anything until we integrate it into a mental model.
New mental models are almost always naive. They are an initial attempt at trying to make sense of something. Mental models only become powerful and sophisticated once they have been applied repeatedly and revised over time to accommodate new data. We revise mental models when they don’t work reliably, we encounter edge cases, we want to broaden the contexts in which they can be applied, or we want to unify several separate models into one general model.
Ideally, we would be actively seeking opportunities to revise our mental models all the time because revising a mental model increases our level of understanding, and improving our ability to revise mental models increases our capacity to learn. But in reality, many of us shy away from revising mental models. We are often emotionally invested in the existing mental model, frightened of feeling destabilized after the existing mental model has been disrupted but before a revised model can take its place, and uncertain if the revised mental model will be any better.
Our reluctance to revise our mental models is often compounded by the horizontal nature of traditional schooling. In schools, most learning happens in silos. Not just silos for subjects, but silos for topics within subjects. We learn something to pass a test, and then we instantly forget it. It’s actually a bit shocking when a teacher references something that you learned a few months ago as though you were suppose to remember it. Horizontal learning discourages us from investing the time and resources required to revise our mental models because we aren’t given the time and we are constantly asked to abandon what we were just building to start something new.
But vertical learning is designed to encourage mental model revision. It challenges and supports us to construct better and better theories over time so that we can understand and do more. It does this by reducing the cost and increasing the benefits of revising a mental model. Starting at an easily accessible entry point, we feel capable and successful when we build on a theory and then find ourselves racing upward and outward on our own. This tips our risk/reward calculation in favor of revision, and helps us learn that we can survive brief periods of destabilization and gain confidence that our revised mental model will be worth the effort.
Modeling diffusion with randomly moving pennies makes diffusion more accessible along multiple dimensions. First, it makes diffusion more concrete. We can understand it on an intuitive level and apply our common sense to reason about it. Second, we don’t have to build a new foundation for it; we can build on top of an existing foundation, which saves time and minimizes the things we need to know. We are more willing to invest in a shared foundation because we know we can leverage it in many different ways.
Third, simulating diffusion creates an immersive experience that stimulates our natural curiosity. It is hard to watch blocks of red dye dissolving in water and not think about what we are observing. When we see something, we look for patterns and want to make sense of it, even if we don’t care about it on a conscious level. That’s just how our brains are wired. Fourth, every simulation is also completely transparent. We can calculate the state of the simulation for any round, which means we can replay time and see and know everything that happens. This invites analysis. Because we can know, we want to know.
Diffusion is more accessible when we make it more concrete, immersive, and transparent, and build it on top of a shared foundation. In turn, this makes it easier, less risky, and less costly to revise our mental model of diffusion. We are much less willing to revise our mental models about something that we perceive as arcane and unknowable.
Vertical learning also works on the reward side, increasing the benefits when we do revise our mental models. For example, when simulating blocks of red dye dissolving in water, we can see that blocks A and B dissolve faster than blocks C and D, and we might theorize that happens because blocks A and B expose more surface area to the water.
That’s a useful mental model, but it doesn’t work in all situations. If we separate the four blocks, blocks A and D dissolve faster than blocks B and C even though all four blocks expose the same amount of surface area to the water.
To understand this new simulation, we need to revise our mental model to also think about the concentration gradients in the water. The blocks of red dye will dissolve faster where there is less red dye already in the water, and that is toward the left, right, and top edges of the water. From there, we can analyze and predict what will happen in other situations.
While this problem may not be intrinsically relevant to students, it is far more interesting than what they typically work on. Imagine a sixth-grader breaking the problem down by sketching isoconcentration maps and estimating diffusion rates by how steep the gradients are. It feels powerful and the student feels successful. And it is a level of thinking that is accessible to all students because the model is concrete, immersive, and transparent, and it builds on top of a shared foundation.
When we extended our model to include solubility, I simply said that enough red dye will dissolve from a block to keep the region around the block saturated. That allowed us to model solubility at a macroscopic scale, but not on a molecular scale. Particles don’t know or care anything about saturation concentrations.
But if we decided to drill down and understand solubility at the molecular scale, then we could model red dye particles transitioning between the solid state and the liquid state along a surface using probabilities, and we could see how and why a system would reach a saturation concentration dynamically. By extending our model and the shared foundation it builds on, we would gain a deeper understanding of solubility and we would be able to solve complex problems where solubility and diffusion are integrated.
Similarly, we could extend our model to simulate reaction rates, since reaction rates are also driven by the probability that reactant particles collide. And from there, we could design and calculate reaction rates in a reaction chamber where reactants are introduced as solid blocks. This is something that I studied as a chemical engineer.
Vertical learning lowers the cost of revising our mental models by making the process easier and more accessible. It also increases the benefits of revising our mental models by enabling us to leverage those mental models to learn and understand more deeply, develop and apply higher-order thinking skills, and solve rich and complex problems. But the ultimate benefit is developing the skills and confidence we need to revise our mental models on our own in life. Because when we do that, we can do anything.
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Summary
A mental model is our internal theory for how and why something works. We learn when we construct new mental models and revise old ones. Even when we read something in a textbook or hear something in a lecture, we don’t actually learn anything until we integrate it into a mental model.
New mental models are almost always naive. They are an initial attempt at trying to make sense of something. Mental models only become powerful and sophisticated once they have been applied repeatedly and revised over time to accommodate new data. We revise mental models when they don’t work reliably, we encounter edge cases, we want to broaden the contexts in which they can be applied, or we want to unify several separate models into one general model.
Ideally, we would be actively seeking opportunities to revise our mental models all the time because revising a mental model increases our level of understanding, and improving our ability to revise mental models increases our capacity to learn. But in reality, many of us shy away from revising mental models. We are often emotionally invested in the existing mental model, frightened of feeling destabilized after the existing mental model has been disrupted but before a revised model can take its place, and uncertain if the revised mental model will be any better.
 |
| Learning horizontally in silos |
Our reluctance to revise our mental models is often compounded by the horizontal nature of traditional schooling. In schools, most learning happens in silos. Not just silos for subjects, but silos for topics within subjects. We learn something to pass a test, and then we instantly forget it. It’s actually a bit shocking when a teacher references something that you learned a few months ago as though you were suppose to remember it. Horizontal learning discourages us from investing the time and resources required to revise our mental models because we aren’t given the time and we are constantly asked to abandon what we were just building to start something new.
 |
| Learning vertically: gaining access through an entry point and then branching up and out |
But vertical learning is designed to encourage mental model revision. It challenges and supports us to construct better and better theories over time so that we can understand and do more. It does this by reducing the cost and increasing the benefits of revising a mental model. Starting at an easily accessible entry point, we feel capable and successful when we build on a theory and then find ourselves racing upward and outward on our own. This tips our risk/reward calculation in favor of revision, and helps us learn that we can survive brief periods of destabilization and gain confidence that our revised mental model will be worth the effort.
Modeling diffusion with randomly moving pennies makes diffusion more accessible along multiple dimensions. First, it makes diffusion more concrete. We can understand it on an intuitive level and apply our common sense to reason about it. Second, we don’t have to build a new foundation for it; we can build on top of an existing foundation, which saves time and minimizes the things we need to know. We are more willing to invest in a shared foundation because we know we can leverage it in many different ways.
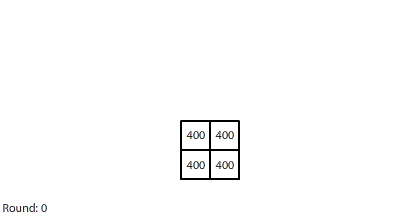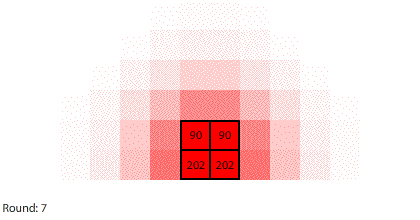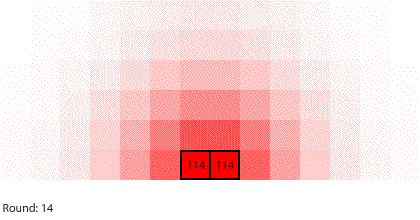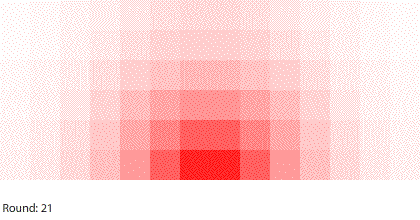 |
| Blocks of red dye dissolving in water |
Third, simulating diffusion creates an immersive experience that stimulates our natural curiosity. It is hard to watch blocks of red dye dissolving in water and not think about what we are observing. When we see something, we look for patterns and want to make sense of it, even if we don’t care about it on a conscious level. That’s just how our brains are wired. Fourth, every simulation is also completely transparent. We can calculate the state of the simulation for any round, which means we can replay time and see and know everything that happens. This invites analysis. Because we can know, we want to know.
Diffusion is more accessible when we make it more concrete, immersive, and transparent, and build it on top of a shared foundation. In turn, this makes it easier, less risky, and less costly to revise our mental model of diffusion. We are much less willing to revise our mental models about something that we perceive as arcane and unknowable.
Vertical learning also works on the reward side, increasing the benefits when we do revise our mental models. For example, when simulating blocks of red dye dissolving in water, we can see that blocks A and B dissolve faster than blocks C and D, and we might theorize that happens because blocks A and B expose more surface area to the water.
 |
| Directions in which the four blocks dissolve |
That’s a useful mental model, but it doesn’t work in all situations. If we separate the four blocks, blocks A and D dissolve faster than blocks B and C even though all four blocks expose the same amount of surface area to the water.
 |
| Four separate blocks of red dye dissolving in water |
 |
| Concentration gradients in the water and directions in which four separate blocks dissolve |
To understand this new simulation, we need to revise our mental model to also think about the concentration gradients in the water. The blocks of red dye will dissolve faster where there is less red dye already in the water, and that is toward the left, right, and top edges of the water. From there, we can analyze and predict what will happen in other situations.
 |
| In what order will the blocks dissolve? Does it matter how far apart the stacks are, or how wide or tall the water is? |
While this problem may not be intrinsically relevant to students, it is far more interesting than what they typically work on. Imagine a sixth-grader breaking the problem down by sketching isoconcentration maps and estimating diffusion rates by how steep the gradients are. It feels powerful and the student feels successful. And it is a level of thinking that is accessible to all students because the model is concrete, immersive, and transparent, and it builds on top of a shared foundation.
When we extended our model to include solubility, I simply said that enough red dye will dissolve from a block to keep the region around the block saturated. That allowed us to model solubility at a macroscopic scale, but not on a molecular scale. Particles don’t know or care anything about saturation concentrations.
But if we decided to drill down and understand solubility at the molecular scale, then we could model red dye particles transitioning between the solid state and the liquid state along a surface using probabilities, and we could see how and why a system would reach a saturation concentration dynamically. By extending our model and the shared foundation it builds on, we would gain a deeper understanding of solubility and we would be able to solve complex problems where solubility and diffusion are integrated.
Similarly, we could extend our model to simulate reaction rates, since reaction rates are also driven by the probability that reactant particles collide. And from there, we could design and calculate reaction rates in a reaction chamber where reactants are introduced as solid blocks. This is something that I studied as a chemical engineer.
Vertical learning lowers the cost of revising our mental models by making the process easier and more accessible. It also increases the benefits of revising our mental models by enabling us to leverage those mental models to learn and understand more deeply, develop and apply higher-order thinking skills, and solve rich and complex problems. But the ultimate benefit is developing the skills and confidence we need to revise our mental models on our own in life. Because when we do that, we can do anything.
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Saturday, February 7, 2015
Statistical Mechanics, Part 7
[This blog post is part of two series. The first series, titled Statistical Mechanics, is a series of lessons that I have developed to illustrate how curriculum and instruction can be designed to encourage vertical learning. We start by drilling down from our understanding of diffusion to develop a dynamic model of diffusion grounded in random particle motion using statistical mechanics. We then build on top of this foundation to construct deeper understandings of fluid flow, heat transfer, and electrical circuits. You can navigate through the lessons in this series using the links below. These lessons are then part of a larger series, Defining Vertical Learning.]
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
So far we have applied our model to simulate the flow of solute particles in diffusion, the flow of electrons in an electrical circuit, and the flow of fluid through pipes. When analyzing diffusion and electrical circuits, we found that a net flow of particles was generated between regions when there was a difference in the number of particles in those regions, and that this behavior at the molecular scale resulted in behavior at the macroscopic scale that matches what we would expect to see in the real world.
If we were to release a gas in an empty container, we would expect to see it spread out just like our red dye did when we dropped it in water.
The major difference is that the red gas particles are moving randomly in a vacuum while the red dye particles are moving randomly through a solvent. We say that there is a net flow of red gas particles down a pressure gradient and there is a net flow of red dye particles down a concentration gradient, but at a molecular scale, there is no such thing as pressure or concentration. Pressure and concentration are measured at a macroscopic scale. At a molecular scale, all we have are particles moving randomly and colliding with one another.
If we simulate the two systems, the models look the same.
For diffusion, we could include solvent particles in our model. If pennies represent red dye particles, we could use nickels to represent water molecules. The nickels would also move randomly left and right, hopping from region to region. But since there are an equal number of nickels in each region, the net flow of water molecules between regions would be zero. The presence of the solvent particles do affect the time and distance scales in our simulation when we calibrate it against reality, but they don’t affect the simulation itself.
If we connect one end of a hose to a pressurized tank of gas and let the gas vent out the other end into a vacuum, our simulation looks a lot like an electrical circuit.
The pressure and number of gas particles in region 1, where the hose is connected to the tank, is high. As we move down the hose and to the right, the pressure and the number of gas particles in each region drops, until both are zero at the end of the hose that is sitting in vacuum. The difference in the number of gas particles in each region generates a net flow of gas particles through the hose. If this were a spaceship in outer space, this net flow of gas particles would thrust the spaceship in the opposite direction.
Our model accurately describes fluid flow when the fluid is a gas, but not when it is a liquid. In a garden hose, there is a pressure drop from the start of the hose to the end of the hose which generates the flow of water, but there isn’t a corresponding drop in the number of water molecules in each region. This is because liquid water is relatively incompressible. Unlike a gas, doubling the pressure on a volume of liquid water does not compress the water and double its density.
At a macroscopic scale, gases and liquids both flow in the same way, which is why they are both classified as fluids. But on a molecular scale, they behave differently. You can still use our model to simulate the flow of liquids, but only if you abstract away the molecular view and think in terms of pressure.
The final kind of flow that we are going to simulate with our model is the flow of heat. To model heat transfer, we are going to use hot and cold particles. In this simulation, we have a tank with hot liquid particles on the left and cold liquid particles on the right.
Over time, the hot and cold particles mix. Because the particles are actually moving from region to region, we are simulating convection. However, the total number of particles in each region isn’t changing because all of the regions have the same number of particles and the net flow of total particles is zero.
Instead of graphing the number of hot and cold particles in a region over time, we can also graph the temperature. Temperature is a measure of the average kinetic energy of the particles in a region, so it is based on the ratio of hot to cold particles. Since the total number of particles in a region isn’t changing, the temperature graph looks just like a graph of the number of hot particles. In heat transfer, heat flows down a temperature gradient.
On the surface, it seems unlikely that we would be able to simulate heat transfer through conduction using our model because, in conduction, heat is transferred through collisions and not the net movement of particles. Our entire model is grounded on random particle motion.
If we are modeling convection, and there are four hot particles and two cold particles in region 4 and two hot particles and four cold particles in region 5, there will be a net flow of one hot particle into region 5 and a net flow of one cold particle into region 4.
But if we are modeling conduction, we say that particles don’t hop from region to region, they collide with particles in the adjacent region and transfer heat. In this case, two hot particles from region 4 collide with two cold particles from region 5 and transfer their heat, and one hot particle from region 5 collides with one cold particle from region 4 and transfers its heat. The particles don’t move (change regions), but heat does.
The last thing we are going to look at is the impact of stirring, or forced convection, on heat transfer. Here we have an ice cube in a glass of water. Over time, the ice cube will cool the water in the glass by absorbing heat from the water. But when the ice cube has absorbed 360 pennies, we are going to say that the ice cube has completely melted away. The 360 pennies represent the heat of fusion.
It takes 19 rounds for the ice cube to melt. What happens if we stir the water?
We are going to model stirring by averaging the heat in regions 4-8. We are basically saying that the stirring evenly distributes the heat in those five regions each round. When we do that, it only takes 18 rounds for the ice cube to melt. Not much difference. What happens if we stir the water more vigorously?
Now it only takes 16 rounds for the ice cube to melt. By stirring the water, we are bringing the warmer water on the right side of the glass closer to the ice cube. This makes the temperature gradient by the ice cube steeper, increasing heat transfer and the flow of heat into the ice cube.
Have you ever wondered what the wind chill factor is and why you feel colder when it is windy outside? Normal human body temperature is approximately 98.6 ˚F, but that isn’t the temperature at our skin. If it is 20 ˚F outside, the cold air is going to cool our skin. And the temperature of the air right next to our skin isn’t going to be 20 ˚F either because heat from our body is going to warm it up. Between our internal temperature of 98.6 ˚F and the external atmospheric temperature of 20 ˚F, there is going to be some form of temperature gradient.
Notice how the temperature gradient passes through four zones. In the first zone, our body maintains a relatively constant body temperature of 98.6 ˚F; in the fourth zone, we have a large mass of air at 20 ˚F; in the second zone, our body is losing heat to the environment; and in the third zone, that heat is warming up the air. The rate of heat transfer from our bodies to the environment is going to depend on the steepness of the gradient in those two middle zones. We call those zones boundary layers because they sit between two zones with different temperatures.
If it is windy outside, the air in the third and fourth zones will be mixed together and the cold 20 ˚F air will be brought closer to the skin. This reduces the width of the boundary layer between the skin and the cold air, increasing the steepness of the temperature gradient and increasing the rate of heat transfer. When it is windy outside, we feel colder because we are physically losing body heat faster.
Boundary layers don’t just apply to temperature gradients. On a hot summer day, the humidity of the air might by 80%, but if sweat is pooling on your skin, the humidity of the air right next to your skin is going to be 100%. Your body’s ability to cool itself by sweating depends on how quickly moisture can diffuse down this concentration gradient. On a nice breezy day, the boundary layer between the 100% humidity at your skin and the 80% humidity in the atmosphere is thinner, so the concentration gradient is steeper and moisture diffuses away faster. This means that, on hot summer days, there are two mechanisms at work that will keep you cooler in a nice breeze: a steeper water concentration gradient and a steeper temperature gradient.
I always like to end a series of lessons with an application problem. Here is a simulation of the temperature gradient in a rectangular heat sink used to cool a microprocessor. When using this heat sink and running at full power, the microprocessor generates 6 pennies of heat in each round and reaches a peak temperature of 102 pennies per region after 3000 rounds. To stay below a peak temperature of 85, 90, or 95 pennies per region with this heat sink, the microprocessor would have to throttle to a lower power state within 1000, 1200, or 1500 rounds, respectively.
Using a chimney-shaped heat sink instead, the microprocessor runs slightly cooler and will reach a peak temperature of 97 pennies per region after 2500 rounds when running at full power. The microprocessor would also be able to run longer before having to throttle to stay below a given peak temperature: within 1100 rounds for 85 pennies per region, 1400 rounds for 90, and 1900 rounds for 95.
The rectangular heat sink and the chimney-shaped heat sink both have the same mass and volume. Can you design a heat sink with the same mass and volume that can keep the microprocessor even cooler? What would the thermal characteristics of the system look like if we added active cooling with a fan blowing across the top?
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Boundary Layers
So far we have applied our model to simulate the flow of solute particles in diffusion, the flow of electrons in an electrical circuit, and the flow of fluid through pipes. When analyzing diffusion and electrical circuits, we found that a net flow of particles was generated between regions when there was a difference in the number of particles in those regions, and that this behavior at the molecular scale resulted in behavior at the macroscopic scale that matches what we would expect to see in the real world.
 |
| There is a net flow of 8 pennies to the right when half of the 38 pennies move to the right and half of the 22 pennies move to the left. |
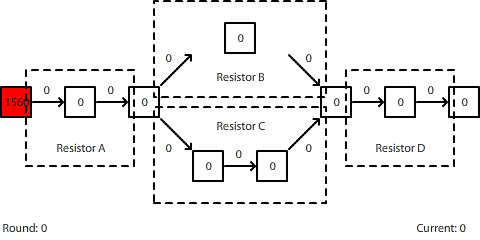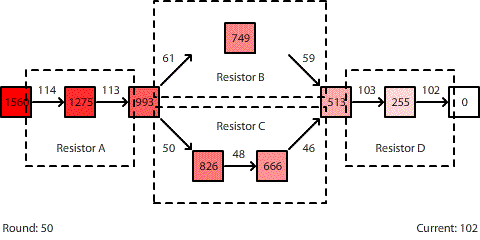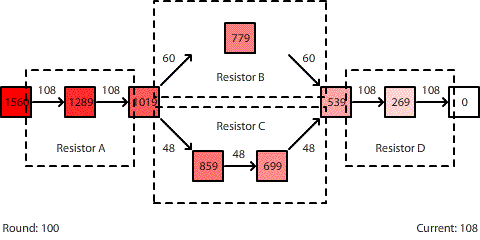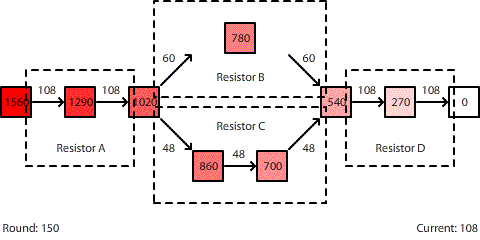 |
| A circuit with four resistors. Resistors B and C are in parallel. The potential difference across the entire circuit is 1560 pennies. |
If we were to release a gas in an empty container, we would expect to see it spread out just like our red dye did when we dropped it in water.
 |
| Red gas filling an empty box |
 |
| Red dye diffusing in a glass of water |
The major difference is that the red gas particles are moving randomly in a vacuum while the red dye particles are moving randomly through a solvent. We say that there is a net flow of red gas particles down a pressure gradient and there is a net flow of red dye particles down a concentration gradient, but at a molecular scale, there is no such thing as pressure or concentration. Pressure and concentration are measured at a macroscopic scale. At a molecular scale, all we have are particles moving randomly and colliding with one another.
If we simulate the two systems, the models look the same.
 |
| Red gas flowing and filling 8 regions |
For diffusion, we could include solvent particles in our model. If pennies represent red dye particles, we could use nickels to represent water molecules. The nickels would also move randomly left and right, hopping from region to region. But since there are an equal number of nickels in each region, the net flow of water molecules between regions would be zero. The presence of the solvent particles do affect the time and distance scales in our simulation when we calibrate it against reality, but they don’t affect the simulation itself.
 |
| Red dye diffusing in water in 8 regions |
If we connect one end of a hose to a pressurized tank of gas and let the gas vent out the other end into a vacuum, our simulation looks a lot like an electrical circuit.
 |
| Hose connected to a pressurized tank of gas at one end and to a vacuum at the other end |
 |
| Pressure and number of particles in an 8-region hose |
The pressure and number of gas particles in region 1, where the hose is connected to the tank, is high. As we move down the hose and to the right, the pressure and the number of gas particles in each region drops, until both are zero at the end of the hose that is sitting in vacuum. The difference in the number of gas particles in each region generates a net flow of gas particles through the hose. If this were a spaceship in outer space, this net flow of gas particles would thrust the spaceship in the opposite direction.
Our model accurately describes fluid flow when the fluid is a gas, but not when it is a liquid. In a garden hose, there is a pressure drop from the start of the hose to the end of the hose which generates the flow of water, but there isn’t a corresponding drop in the number of water molecules in each region. This is because liquid water is relatively incompressible. Unlike a gas, doubling the pressure on a volume of liquid water does not compress the water and double its density.
At a macroscopic scale, gases and liquids both flow in the same way, which is why they are both classified as fluids. But on a molecular scale, they behave differently. You can still use our model to simulate the flow of liquids, but only if you abstract away the molecular view and think in terms of pressure.
The final kind of flow that we are going to simulate with our model is the flow of heat. To model heat transfer, we are going to use hot and cold particles. In this simulation, we have a tank with hot liquid particles on the left and cold liquid particles on the right.
 |
| Hot and cold particles mixing |
Over time, the hot and cold particles mix. Because the particles are actually moving from region to region, we are simulating convection. However, the total number of particles in each region isn’t changing because all of the regions have the same number of particles and the net flow of total particles is zero.
 |
| Temperature gradient of the system as the hot and cold particles mix |
Instead of graphing the number of hot and cold particles in a region over time, we can also graph the temperature. Temperature is a measure of the average kinetic energy of the particles in a region, so it is based on the ratio of hot to cold particles. Since the total number of particles in a region isn’t changing, the temperature graph looks just like a graph of the number of hot particles. In heat transfer, heat flows down a temperature gradient.
On the surface, it seems unlikely that we would be able to simulate heat transfer through conduction using our model because, in conduction, heat is transferred through collisions and not the net movement of particles. Our entire model is grounded on random particle motion.
 |
| Heat transfer through convection |
If we are modeling convection, and there are four hot particles and two cold particles in region 4 and two hot particles and four cold particles in region 5, there will be a net flow of one hot particle into region 5 and a net flow of one cold particle into region 4.
 |
| Heat transfer through conduction |
But if we are modeling conduction, we say that particles don’t hop from region to region, they collide with particles in the adjacent region and transfer heat. In this case, two hot particles from region 4 collide with two cold particles from region 5 and transfer their heat, and one hot particle from region 5 collides with one cold particle from region 4 and transfers its heat. The particles don’t move (change regions), but heat does.
 |
| Heat transfer in a metal rod through conduction when the left end of the rod is dunked in a bath of ice water |
The last thing we are going to look at is the impact of stirring, or forced convection, on heat transfer. Here we have an ice cube in a glass of water. Over time, the ice cube will cool the water in the glass by absorbing heat from the water. But when the ice cube has absorbed 360 pennies, we are going to say that the ice cube has completely melted away. The 360 pennies represent the heat of fusion.
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side |
It takes 19 rounds for the ice cube to melt. What happens if we stir the water?
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side and the water being stirred |
We are going to model stirring by averaging the heat in regions 4-8. We are basically saying that the stirring evenly distributes the heat in those five regions each round. When we do that, it only takes 18 rounds for the ice cube to melt. Not much difference. What happens if we stir the water more vigorously?
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side and the water being stirred more vigorously |
Now it only takes 16 rounds for the ice cube to melt. By stirring the water, we are bringing the warmer water on the right side of the glass closer to the ice cube. This makes the temperature gradient by the ice cube steeper, increasing heat transfer and the flow of heat into the ice cube.
Have you ever wondered what the wind chill factor is and why you feel colder when it is windy outside? Normal human body temperature is approximately 98.6 ˚F, but that isn’t the temperature at our skin. If it is 20 ˚F outside, the cold air is going to cool our skin. And the temperature of the air right next to our skin isn’t going to be 20 ˚F either because heat from our body is going to warm it up. Between our internal temperature of 98.6 ˚F and the external atmospheric temperature of 20 ˚F, there is going to be some form of temperature gradient.
 |
| Temperature gradient from internal body temperature to external atmospheric temperature |
Notice how the temperature gradient passes through four zones. In the first zone, our body maintains a relatively constant body temperature of 98.6 ˚F; in the fourth zone, we have a large mass of air at 20 ˚F; in the second zone, our body is losing heat to the environment; and in the third zone, that heat is warming up the air. The rate of heat transfer from our bodies to the environment is going to depend on the steepness of the gradient in those two middle zones. We call those zones boundary layers because they sit between two zones with different temperatures.
 |
| Temperature gradient from internal body temperature to external atmospheric temperature in windy conditions |
If it is windy outside, the air in the third and fourth zones will be mixed together and the cold 20 ˚F air will be brought closer to the skin. This reduces the width of the boundary layer between the skin and the cold air, increasing the steepness of the temperature gradient and increasing the rate of heat transfer. When it is windy outside, we feel colder because we are physically losing body heat faster.
Boundary layers don’t just apply to temperature gradients. On a hot summer day, the humidity of the air might by 80%, but if sweat is pooling on your skin, the humidity of the air right next to your skin is going to be 100%. Your body’s ability to cool itself by sweating depends on how quickly moisture can diffuse down this concentration gradient. On a nice breezy day, the boundary layer between the 100% humidity at your skin and the 80% humidity in the atmosphere is thinner, so the concentration gradient is steeper and moisture diffuses away faster. This means that, on hot summer days, there are two mechanisms at work that will keep you cooler in a nice breeze: a steeper water concentration gradient and a steeper temperature gradient.
I always like to end a series of lessons with an application problem. Here is a simulation of the temperature gradient in a rectangular heat sink used to cool a microprocessor. When using this heat sink and running at full power, the microprocessor generates 6 pennies of heat in each round and reaches a peak temperature of 102 pennies per region after 3000 rounds. To stay below a peak temperature of 85, 90, or 95 pennies per region with this heat sink, the microprocessor would have to throttle to a lower power state within 1000, 1200, or 1500 rounds, respectively.
 |
| Temperature gradient in a rectangular heat sink used to cool a microprocessor |
Using a chimney-shaped heat sink instead, the microprocessor runs slightly cooler and will reach a peak temperature of 97 pennies per region after 2500 rounds when running at full power. The microprocessor would also be able to run longer before having to throttle to stay below a given peak temperature: within 1100 rounds for 85 pennies per region, 1400 rounds for 90, and 1900 rounds for 95.
 |
| Temperature gradient in a chimney-shaped heat sink cooling the same microprocessor |
The rectangular heat sink and the chimney-shaped heat sink both have the same mass and volume. Can you design a heat sink with the same mass and volume that can keep the microprocessor even cooler? What would the thermal characteristics of the system look like if we added active cooling with a fan blowing across the top?
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Subscribe to:
Posts (Atom)