Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Boundary Layers
So far we have applied our model to simulate the flow of solute particles in diffusion, the flow of electrons in an electrical circuit, and the flow of fluid through pipes. When analyzing diffusion and electrical circuits, we found that a net flow of particles was generated between regions when there was a difference in the number of particles in those regions, and that this behavior at the molecular scale resulted in behavior at the macroscopic scale that matches what we would expect to see in the real world.
 |
| There is a net flow of 8 pennies to the right when half of the 38 pennies move to the right and half of the 22 pennies move to the left. |
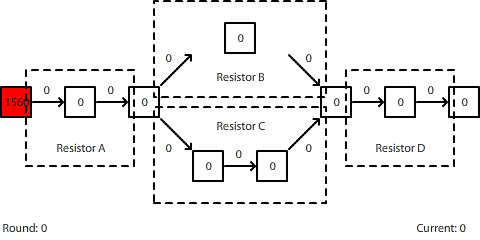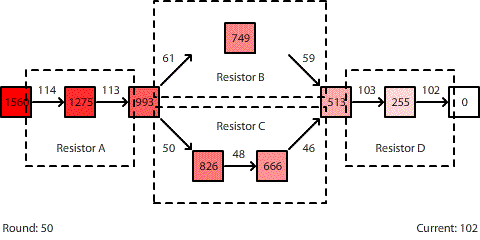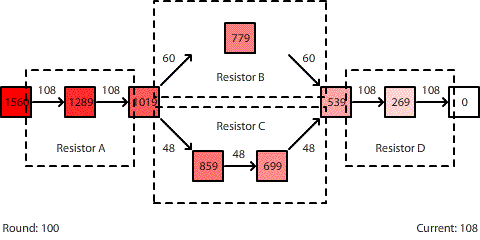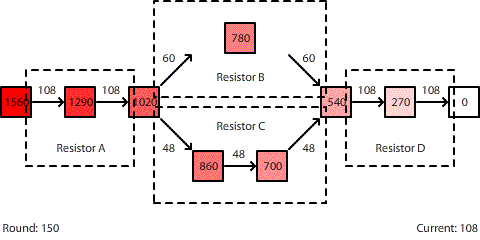 |
| A circuit with four resistors. Resistors B and C are in parallel. The potential difference across the entire circuit is 1560 pennies. |
If we were to release a gas in an empty container, we would expect to see it spread out just like our red dye did when we dropped it in water.
 |
| Red gas filling an empty box |
 |
| Red dye diffusing in a glass of water |
The major difference is that the red gas particles are moving randomly in a vacuum while the red dye particles are moving randomly through a solvent. We say that there is a net flow of red gas particles down a pressure gradient and there is a net flow of red dye particles down a concentration gradient, but at a molecular scale, there is no such thing as pressure or concentration. Pressure and concentration are measured at a macroscopic scale. At a molecular scale, all we have are particles moving randomly and colliding with one another.
If we simulate the two systems, the models look the same.
 |
| Red gas flowing and filling 8 regions |
For diffusion, we could include solvent particles in our model. If pennies represent red dye particles, we could use nickels to represent water molecules. The nickels would also move randomly left and right, hopping from region to region. But since there are an equal number of nickels in each region, the net flow of water molecules between regions would be zero. The presence of the solvent particles do affect the time and distance scales in our simulation when we calibrate it against reality, but they don’t affect the simulation itself.
 |
| Red dye diffusing in water in 8 regions |
If we connect one end of a hose to a pressurized tank of gas and let the gas vent out the other end into a vacuum, our simulation looks a lot like an electrical circuit.
 |
| Hose connected to a pressurized tank of gas at one end and to a vacuum at the other end |
 |
| Pressure and number of particles in an 8-region hose |
The pressure and number of gas particles in region 1, where the hose is connected to the tank, is high. As we move down the hose and to the right, the pressure and the number of gas particles in each region drops, until both are zero at the end of the hose that is sitting in vacuum. The difference in the number of gas particles in each region generates a net flow of gas particles through the hose. If this were a spaceship in outer space, this net flow of gas particles would thrust the spaceship in the opposite direction.
Our model accurately describes fluid flow when the fluid is a gas, but not when it is a liquid. In a garden hose, there is a pressure drop from the start of the hose to the end of the hose which generates the flow of water, but there isn’t a corresponding drop in the number of water molecules in each region. This is because liquid water is relatively incompressible. Unlike a gas, doubling the pressure on a volume of liquid water does not compress the water and double its density.
At a macroscopic scale, gases and liquids both flow in the same way, which is why they are both classified as fluids. But on a molecular scale, they behave differently. You can still use our model to simulate the flow of liquids, but only if you abstract away the molecular view and think in terms of pressure.
The final kind of flow that we are going to simulate with our model is the flow of heat. To model heat transfer, we are going to use hot and cold particles. In this simulation, we have a tank with hot liquid particles on the left and cold liquid particles on the right.
 |
| Hot and cold particles mixing |
Over time, the hot and cold particles mix. Because the particles are actually moving from region to region, we are simulating convection. However, the total number of particles in each region isn’t changing because all of the regions have the same number of particles and the net flow of total particles is zero.
 |
| Temperature gradient of the system as the hot and cold particles mix |
Instead of graphing the number of hot and cold particles in a region over time, we can also graph the temperature. Temperature is a measure of the average kinetic energy of the particles in a region, so it is based on the ratio of hot to cold particles. Since the total number of particles in a region isn’t changing, the temperature graph looks just like a graph of the number of hot particles. In heat transfer, heat flows down a temperature gradient.
On the surface, it seems unlikely that we would be able to simulate heat transfer through conduction using our model because, in conduction, heat is transferred through collisions and not the net movement of particles. Our entire model is grounded on random particle motion.
 |
| Heat transfer through convection |
If we are modeling convection, and there are four hot particles and two cold particles in region 4 and two hot particles and four cold particles in region 5, there will be a net flow of one hot particle into region 5 and a net flow of one cold particle into region 4.
 |
| Heat transfer through conduction |
But if we are modeling conduction, we say that particles don’t hop from region to region, they collide with particles in the adjacent region and transfer heat. In this case, two hot particles from region 4 collide with two cold particles from region 5 and transfer their heat, and one hot particle from region 5 collides with one cold particle from region 4 and transfers its heat. The particles don’t move (change regions), but heat does.
 |
| Heat transfer in a metal rod through conduction when the left end of the rod is dunked in a bath of ice water |
The last thing we are going to look at is the impact of stirring, or forced convection, on heat transfer. Here we have an ice cube in a glass of water. Over time, the ice cube will cool the water in the glass by absorbing heat from the water. But when the ice cube has absorbed 360 pennies, we are going to say that the ice cube has completely melted away. The 360 pennies represent the heat of fusion.
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side |
It takes 19 rounds for the ice cube to melt. What happens if we stir the water?
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side and the water being stirred |
We are going to model stirring by averaging the heat in regions 4-8. We are basically saying that the stirring evenly distributes the heat in those five regions each round. When we do that, it only takes 18 rounds for the ice cube to melt. Not much difference. What happens if we stir the water more vigorously?
 |
| Temperature gradient of a glass of water with an ice cube melting on the left side and the water being stirred more vigorously |
Now it only takes 16 rounds for the ice cube to melt. By stirring the water, we are bringing the warmer water on the right side of the glass closer to the ice cube. This makes the temperature gradient by the ice cube steeper, increasing heat transfer and the flow of heat into the ice cube.
Have you ever wondered what the wind chill factor is and why you feel colder when it is windy outside? Normal human body temperature is approximately 98.6 ˚F, but that isn’t the temperature at our skin. If it is 20 ˚F outside, the cold air is going to cool our skin. And the temperature of the air right next to our skin isn’t going to be 20 ˚F either because heat from our body is going to warm it up. Between our internal temperature of 98.6 ˚F and the external atmospheric temperature of 20 ˚F, there is going to be some form of temperature gradient.
 |
| Temperature gradient from internal body temperature to external atmospheric temperature |
Notice how the temperature gradient passes through four zones. In the first zone, our body maintains a relatively constant body temperature of 98.6 ˚F; in the fourth zone, we have a large mass of air at 20 ˚F; in the second zone, our body is losing heat to the environment; and in the third zone, that heat is warming up the air. The rate of heat transfer from our bodies to the environment is going to depend on the steepness of the gradient in those two middle zones. We call those zones boundary layers because they sit between two zones with different temperatures.
 |
| Temperature gradient from internal body temperature to external atmospheric temperature in windy conditions |
If it is windy outside, the air in the third and fourth zones will be mixed together and the cold 20 ˚F air will be brought closer to the skin. This reduces the width of the boundary layer between the skin and the cold air, increasing the steepness of the temperature gradient and increasing the rate of heat transfer. When it is windy outside, we feel colder because we are physically losing body heat faster.
Boundary layers don’t just apply to temperature gradients. On a hot summer day, the humidity of the air might by 80%, but if sweat is pooling on your skin, the humidity of the air right next to your skin is going to be 100%. Your body’s ability to cool itself by sweating depends on how quickly moisture can diffuse down this concentration gradient. On a nice breezy day, the boundary layer between the 100% humidity at your skin and the 80% humidity in the atmosphere is thinner, so the concentration gradient is steeper and moisture diffuses away faster. This means that, on hot summer days, there are two mechanisms at work that will keep you cooler in a nice breeze: a steeper water concentration gradient and a steeper temperature gradient.
I always like to end a series of lessons with an application problem. Here is a simulation of the temperature gradient in a rectangular heat sink used to cool a microprocessor. When using this heat sink and running at full power, the microprocessor generates 6 pennies of heat in each round and reaches a peak temperature of 102 pennies per region after 3000 rounds. To stay below a peak temperature of 85, 90, or 95 pennies per region with this heat sink, the microprocessor would have to throttle to a lower power state within 1000, 1200, or 1500 rounds, respectively.
 |
| Temperature gradient in a rectangular heat sink used to cool a microprocessor |
Using a chimney-shaped heat sink instead, the microprocessor runs slightly cooler and will reach a peak temperature of 97 pennies per region after 2500 rounds when running at full power. The microprocessor would also be able to run longer before having to throttle to stay below a given peak temperature: within 1100 rounds for 85 pennies per region, 1400 rounds for 90, and 1900 rounds for 95.
 |
| Temperature gradient in a chimney-shaped heat sink cooling the same microprocessor |
The rectangular heat sink and the chimney-shaped heat sink both have the same mass and volume. Can you design a heat sink with the same mass and volume that can keep the microprocessor even cooler? What would the thermal characteristics of the system look like if we added active cooling with a fan blowing across the top?
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
No comments:
Post a Comment