Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
Summary
A mental model is our internal theory for how and why something works. We learn when we construct new mental models and revise old ones. Even when we read something in a textbook or hear something in a lecture, we don’t actually learn anything until we integrate it into a mental model.
New mental models are almost always naive. They are an initial attempt at trying to make sense of something. Mental models only become powerful and sophisticated once they have been applied repeatedly and revised over time to accommodate new data. We revise mental models when they don’t work reliably, we encounter edge cases, we want to broaden the contexts in which they can be applied, or we want to unify several separate models into one general model.
Ideally, we would be actively seeking opportunities to revise our mental models all the time because revising a mental model increases our level of understanding, and improving our ability to revise mental models increases our capacity to learn. But in reality, many of us shy away from revising mental models. We are often emotionally invested in the existing mental model, frightened of feeling destabilized after the existing mental model has been disrupted but before a revised model can take its place, and uncertain if the revised mental model will be any better.
 |
| Learning horizontally in silos |
Our reluctance to revise our mental models is often compounded by the horizontal nature of traditional schooling. In schools, most learning happens in silos. Not just silos for subjects, but silos for topics within subjects. We learn something to pass a test, and then we instantly forget it. It’s actually a bit shocking when a teacher references something that you learned a few months ago as though you were suppose to remember it. Horizontal learning discourages us from investing the time and resources required to revise our mental models because we aren’t given the time and we are constantly asked to abandon what we were just building to start something new.
 |
| Learning vertically: gaining access through an entry point and then branching up and out |
But vertical learning is designed to encourage mental model revision. It challenges and supports us to construct better and better theories over time so that we can understand and do more. It does this by reducing the cost and increasing the benefits of revising a mental model. Starting at an easily accessible entry point, we feel capable and successful when we build on a theory and then find ourselves racing upward and outward on our own. This tips our risk/reward calculation in favor of revision, and helps us learn that we can survive brief periods of destabilization and gain confidence that our revised mental model will be worth the effort.
Modeling diffusion with randomly moving pennies makes diffusion more accessible along multiple dimensions. First, it makes diffusion more concrete. We can understand it on an intuitive level and apply our common sense to reason about it. Second, we don’t have to build a new foundation for it; we can build on top of an existing foundation, which saves time and minimizes the things we need to know. We are more willing to invest in a shared foundation because we know we can leverage it in many different ways.
 |
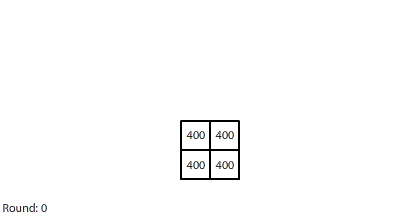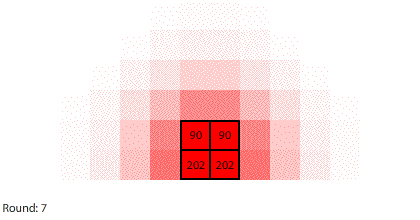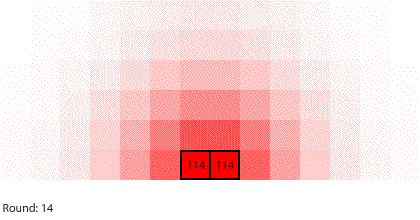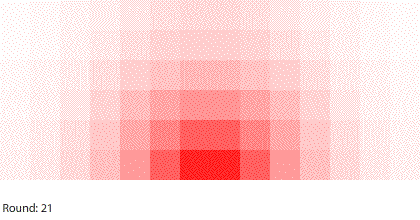| Blocks of red dye dissolving in water |
Third, simulating diffusion creates an immersive experience that stimulates our natural curiosity. It is hard to watch blocks of red dye dissolving in water and not think about what we are observing. When we see something, we look for patterns and want to make sense of it, even if we don’t care about it on a conscious level. That’s just how our brains are wired. Fourth, every simulation is also completely transparent. We can calculate the state of the simulation for any round, which means we can replay time and see and know everything that happens. This invites analysis. Because we can know, we want to know.
Diffusion is more accessible when we make it more concrete, immersive, and transparent, and build it on top of a shared foundation. In turn, this makes it easier, less risky, and less costly to revise our mental model of diffusion. We are much less willing to revise our mental models about something that we perceive as arcane and unknowable.
Vertical learning also works on the reward side, increasing the benefits when we do revise our mental models. For example, when simulating blocks of red dye dissolving in water, we can see that blocks A and B dissolve faster than blocks C and D, and we might theorize that happens because blocks A and B expose more surface area to the water.
 |
| Directions in which the four blocks dissolve |
That’s a useful mental model, but it doesn’t work in all situations. If we separate the four blocks, blocks A and D dissolve faster than blocks B and C even though all four blocks expose the same amount of surface area to the water.
 |
| Four separate blocks of red dye dissolving in water |
 |
| Concentration gradients in the water and directions in which four separate blocks dissolve |
To understand this new simulation, we need to revise our mental model to also think about the concentration gradients in the water. The blocks of red dye will dissolve faster where there is less red dye already in the water, and that is toward the left, right, and top edges of the water. From there, we can analyze and predict what will happen in other situations.
 |
| In what order will the blocks dissolve? Does it matter how far apart the stacks are, or how wide or tall the water is? |
While this problem may not be intrinsically relevant to students, it is far more interesting than what they typically work on. Imagine a sixth-grader breaking the problem down by sketching isoconcentration maps and estimating diffusion rates by how steep the gradients are. It feels powerful and the student feels successful. And it is a level of thinking that is accessible to all students because the model is concrete, immersive, and transparent, and it builds on top of a shared foundation.
When we extended our model to include solubility, I simply said that enough red dye will dissolve from a block to keep the region around the block saturated. That allowed us to model solubility at a macroscopic scale, but not on a molecular scale. Particles don’t know or care anything about saturation concentrations.
 |
| At a molecular scale, there is a probability that a particle in the solid state will transition to the liquid state, and a probability that a particle in the liquid state will transition to the solid state. |
But if we decided to drill down and understand solubility at the molecular scale, then we could model red dye particles transitioning between the solid state and the liquid state along a surface using probabilities, and we could see how and why a system would reach a saturation concentration dynamically. By extending our model and the shared foundation it builds on, we would gain a deeper understanding of solubility and we would be able to solve complex problems where solubility and diffusion are integrated.
Similarly, we could extend our model to simulate reaction rates, since reaction rates are also driven by the probability that reactant particles collide. And from there, we could design and calculate reaction rates in a reaction chamber where reactants are introduced as solid blocks. This is something that I studied as a chemical engineer.
Vertical learning lowers the cost of revising our mental models by making the process easier and more accessible. It also increases the benefits of revising our mental models by enabling us to leverage those mental models to learn and understand more deeply, develop and apply higher-order thinking skills, and solve rich and complex problems. But the ultimate benefit is developing the skills and confidence we need to revise our mental models on our own in life. Because when we do that, we can do anything.
Part 1 | Part 2 | Part 3 | Part 4 | Part 5 | Part 6 | Part 7 | Summary
No comments:
Post a Comment